OptiStruct&HyperStudy全局搜索功能

求解优化问题后，常见的一个讨论是所得到的解是局部最优解还是全局最优解。基于局部近似的算法（如梯度优化算法）更易于找到一个局部最优解，而全局近似算法（如响应面算法）和全局探索算法（如遗传算法）则更有可能找到局部最优解之外的解，也就是说，全局类算法提高了找到全局最优解的机会。可是没有算法可以保证其最优解是真正的全局最优解，除非该优化问题为凸问题。所谓凸优化问题，其目标函数和可行区域需要是凸的，可惜实际中大多数工程问题并非凸问题。因此，对于实际问题，全局最优解仍然难以找到。不同的算法只是改变找到全局最优解的机会，但无法确保找到。此外，值得注意的是，任何提高找到全局最优解机会的算法都会增加计算成本，而且通常是大大增加。

图1-2描述了凸问题的概念。凸优化问题只有一个最小值（或最大值），这个最小值（图中A点）即是全局最小值。

用基于梯度的算法求解非凸优化问题时，结果依赖于起始点，这类算法更易于找到局部最优解。OptiStruct11.0在梯度算法的基础上开发了新的全局搜索算法，称为“多起点优化”。该算法通过从多个起点执行优化，广泛地在设计空间中探索最优解，有效地提高了找到全局最优解的可能性。由于优化结果依赖于起始点，n个不同的起始点可能找到n个不同的优化结果。当然不同的起始点也有可能找到同一个最优解，但是这不意味着所找到的最优解一定是全局最优解，如图1-3所示。

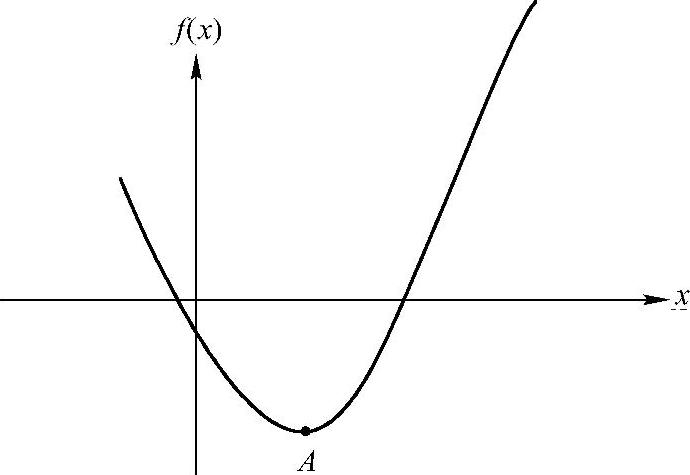
图1-2 凸函数，f（x）(www.xing528.com)

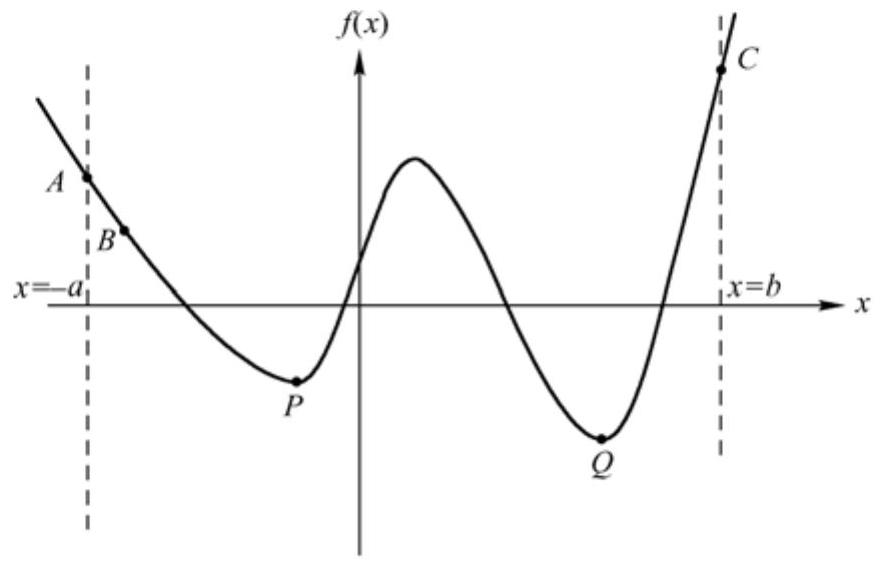
图1-3 非凸函数，f（x）

考虑非凸函数f（x），定义域为­a≤x≤b。如果从A点开始优化，最优解将是P点。从B点开始优化，最优解同样是P点。而如果从C点开始优化，最优解将是Q点。由此可以看出，多起点优化算法并不能保证找到全局最优解（当然其他任何算法也是如此），但是它可以提高找到全局最优解的可能性。

OptiStruct11.0里全局搜索优化（Global Search Option，GSO）支持上述算法。全局搜索优化通过输入文件中I/O块里的DGLOBAL选项设置，相应的参数通过BULKDATA中的DGLOBAL卡片定义。