近自由电子近似及其波函数-固体物理学习指导

1.模型

（1）电子在一个周期性势场中自由运动（单电子模型）。

（2）关于势场的假定：周期性势场随距离的变化很小，可用量子力学中的微扰法来处理。即

由于势场随距离的变化很小，即弱周期性势场中电子受到的作用和恒定势场时差不多，因此称为近自由电子近似。在处理过程中，可把自由电子的波函数作为零级近似波函数。

2.零级近似的波动方程、波函数与能量

以一维为例。考虑一根长为L 的一维晶体，具有N 个原胞，则有L=Na。薛定谔方程为

能量本征值，且波矢，n=0，±1，±2，…。

显然，零级近似下的解为自由电子，能量本征值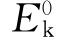作为k的函数，具有抛物线形式，所以称为近自由电子近似。

3.考虑到微扰后的波动方程、波函数与能量（非简并）

根据微扰论，系统哈密顿量为

该波函数代表波矢为k 的前进的平面波，以及被周期性势场所散射的波的叠加，另外，系统能量为

在一般情况下，由各原子所产生的散射波的位相之间没有什么关系，散射波振幅很小，且可以彼此相互抵消，周期性势场对于前进的平面波影响不大，这正是非简并微扰论适用的情况。

4.简并情况下的波函数和能量

显然，零级近似波函数是一种前进波和反射波迭加而成的驻波。这两种波的振幅相同，位相也相同，只是方向相反。其原因是，k=时，原子实对电子波的衍射作用强烈到如此程度，以至于沿任何一个方向前进都不可能。综上，k=即nλ=2a，正好满足布拉格条件，2dsinθ=nλ。显然在d→a，θ→时电子遭到全反射，具有这种波长的电子不能在晶体中运动，此时电子速度v=0，没有动能只有势能。

能量为

周期场中电子的能级形成能带是能带论最基本的结果之一。我们将看到，正是这个结论，提供了导体和非导体的理论解释。各能带之间的间隔称为 “带隙”或 “禁带”。在带隙中不存在能级。(www.xing528.com)

5.准连续能级和能带

根据前述讨论，k只能取一些分立值k=，对应每一个l应有一个能级。当N 很大时，k的取值是十分密集的，相应的能级也同样十分密集，因此称为准连续能级。最重要的特点是准连续的能级分裂为一系列由允许带和禁带组成的能带。

6.能带中的量子态数目

由于每个k值在k 空间所占线度为，各能带所对应的k 值范围是，所以每个能带所包含的k值数目为=N，等于正格子中原胞的数目，计入自旋，每个能带中包含有2N 个量子态。

7.简约波矢与能带的关系

在一维关系曲线中，可以通过平移把线段a由［π/a，2π/a］移至 ［-π/a，0］，成为线段a′，从而可以把第二布里渊区中的E-k 关系曲线a，用简约布里渊区中的a′来表示。

同理其他布里渊区的线段也可以做相应的移动。在一维情况下，我们可以把这种移动表示为k=+k，其中m 为整数。其中k 为任一布里渊区中的波矢，k 为简约布里渊区中的相应波矢，称为简约波矢。从而可把布洛赫函数ψk（x）=eikxu（x）表示为ψk（x）=由于是一个周期函数，所以中括号内的函数仍为一周期函数。

因此，每一个能带中的各状态对应于在间不同的简约波矢k，而一个简约波矢k 则对应能量高低不同的一系列状态，分别属于能带1，2，3，…。所以一般地标志一个状态需要标明：①它属于哪一个能带；②它的简约波矢k 等于什么？

8.能带的简约区、扩展区和周期区图

描述固体能带结构有三种图式：

（1）简约区图：将不同能带平移适当的倒格矢进入到第一布里渊区内表示（在简约布里渊区内画出所有能带）。

（2）扩展区图：在不同的布里渊区画出不同的能带。

（3）周期区图：在每一个布里渊区周期性地画出所有能带（强调任一特定的波矢k 的能量可以用和它相差Kh的波矢来描述）。

每个布里渊区中波矢k 可取N 个值，而能带序号越小，能带宽度越小，故能带序号越小，能态密度越大。