金属自由电子气的量子理论简介

1.自由电子的状态描述——波函数、能级及波矢

根据索末菲模型的基本假设，可将一个复杂的强关联的多体问题，转化为在平均势场中运动的单电子问题。

其中，正离子提供电荷以满足整个系统是电中性的；每个电子所具有的状态就是一定深度的方势阱中运动的粒子所具存的能态，称为单电子本征态。在求得单电子能级的基础上，利用泡利不相容原理，将N 个电子填充到这些能级中，获得N 电子系统的基态。另外，遵从费米—狄拉克分布的自由电子在运动过程中被认为存在一定的散射机制。

考虑温度T=0K 时，含有N 个自由电子的边长为L 的立方体金属系统。电子在金属中的势能取值

单电子的运动状态用波函数ψ（r）描述。求解定态薛定谔方程：

容易求得电子波函数和相应的能量为

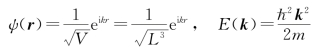
不难证明，电子具有确定的动量和相应的电子速度v=这个速度就是波的群速度，也就是说，金属中电子的自由运动速度与波的群速度一致。

结合周期性边界条件，单个电子波函数表示的是行进的平面波。

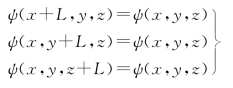
可以求得波矢为

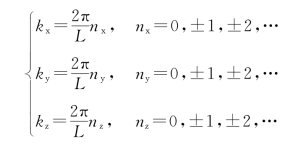
可见，边界条件的引入，只允许波矢k 取分立值。当L→∞时，金属中电子的行进平面波状态自然过渡到无限空间的平面波状态。波矢从由上式确定的分立取值过渡到连续变化的取值。

于是可以进一步得到波函数ψ（r）=以及能量。这表面，一组nx，ny，nz的取值就给出了电子的一个状态和对应的能量值，这个能量值对应着一个能级。对于同一个能量值，有多种不同的组合取值，即同一个能量值有多个状态与之对应。多个状态对应同一个能级，则该能级称为简并能级。

在波矢为k 的行波状态下，电子具有确定的动量和速度；由于平面波的波矢k 的量子化，因此单电子的本征能量、动量和速度均取分立值，即量子化。

2.金属中自由电子的态密度

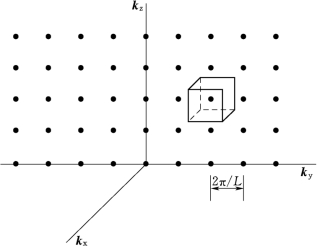
图6-2　状态代表点在k空间的分布

我们把波矢看作是空间矢量，相应的空间称为波矢空间（也称k 空间），如图6-2所示。在以kx，ky，kz为坐标轴的k 空间中，许可的取值（或状态）用分立点表示，每个点在k 空间占据的体积相等，为

根据量子力学原理，电子在分立能级上的分布规则：

（1）电子在能级上的填充遵守泡利不相容原理。

（2）T=0K，电子从最低能级开始填充（能量最低原理）；每个能级可以填2个电子（自旋参量）；能量相同的电子态数目称为简并度。

（3）电子填充的最高能级称为费米能级EF。

定义能态密度g（E）（也称能量态密度）为：在单位体积、单位能量间隔内允许存在的量子态数目。

而在k 到k+dk 的球壳体积元中，电子状态（含自旋态）的数目：

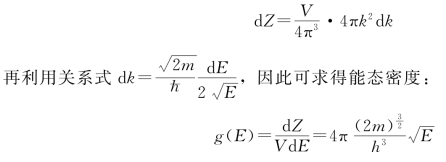
注：在相当一部分教材中，能态密度被定义为 “单位能量间隔内的电子状态数”，即g（E）=事实上这与通过等能面体积元法（参考第四章中的频谱密度求法）求得的能态密度定义相通。当然，本书出于与陆栋教材一致的考虑，仍旧采用g（E）=的计算方法。从物理思想上两者并没有对错之分。

3.费米-狄拉克分布函数

由统计物理知，具有能量为E 的状态被电子占据的几率用费米-狄拉克分布函数表示为

式中：EF为费米能级，它的意义是在体积不变的条件下，系统增加一个电子所需的自由能。

在有限温度下，能量介于E～E+dE 间各状态拥有的电子数：

系统总的电子数：(www.xing528.com)

4.T=0K 时（电子处于基态下）的费米能——费米球、费米面、费米波矢

根据泡利不相容原理，k 空间内每个允许的k 态上只可容纳两个自旋方向相反的电子。因此含有N 个电子的电子气系统，它的最低能量状态（也称基态）对应于k 空间中具有最低能量的个状态点。在T=0K 时，N 个电子的基态是从能量最低的状态点由低到高依次填充得到。

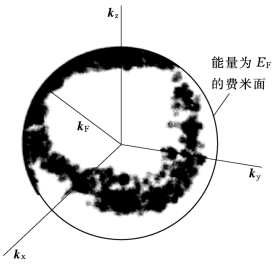
图6-3　N 个自由电子的基态

由于单电子能级E（k）=，且N 的数目很大，因此这些具有最低能量的个状态点占据区域最后形成一个球，一般称为费米球，其半径称为费米波矢kF，如图6-3所示。

在基态时，费米球内的所有状态都被电子占据，而球外的状态全部未被电子占据。在k 空间中将占据态与未占据态分隔的界面，称为费米面。费米面是近代金属理论的重要基本概念，一般来讲，它不是球形。

定义单位体积中的平均电子数为电子数密度n，且电子数N=不难解得T=0K时费米波矢：

而处于费米面上单电子态的能量（称为费米能级EF）在基态下的表达式为

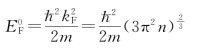
这样还可以依次推出相应的费米动量、费米速度和费米温度：

另外可以推出重要的物理量——费米面的能态密度g（EF）满足：

还有基态单电子平均能量：

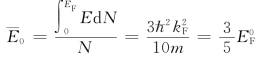
该式说明：

（1）T=0K 时，电子填充的最高能级EF与电子数密度n有关。

（2）T=0K 时，电子仍具有相当大的平均能量。

（3）在经典统计中，当T=0K 时，所有的电子的能量都等于零；而量子统计指出，当T=0K 时，电子的费米能量不是零，而是几个电子伏特。这是因为，电子遵从泡利不相容原理，每个能级只能容纳自旋相反的两个电子，所以即使T=0K，电子也不可能全部填充在最低的能级上。

5.T≠0K（低温状态）时的费米能

当T≠0K 时，自由电子气体的状态称为热激发态。由于热激发能近似等于kBT，这个能量仅有费米能的几百分之一，因此仅有费米面内约kBT 能量范围内的电子由于获得能量而可能跃迁到费米面以外的空状态上去。此时电子的分布与基态情况不同。下图6-4为费米分布f（E）-E 曲线，图6-5为费米面与激发态的示意图。

根据相关计算，可以得出T≠0K 时费米能的公式：

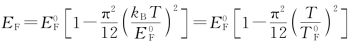
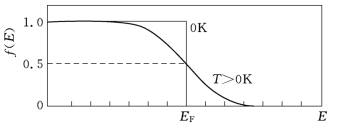
图6-4　费米分布曲线

这个公式说明：

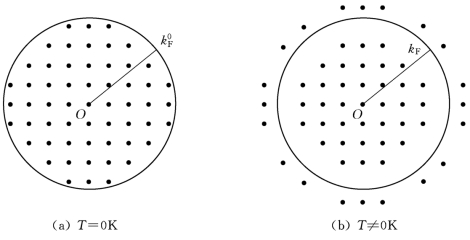
图6-5　费米面和激发态（·为电子占据的一个状态）

（3）实验证明EF随温度的微小变化往往对金属的物理性质有重要影响。

综上，对于金属而言，由于T≪TF=总是成立的，因此，只有费米面以内约kBT能量范围的一小部分电子可以被激发到高能态，而离费米面较远的电子则仍保持原来（T=0K）的状态（即基态），我们称这部分电子被“冷冻” 下来。

因此，虽然金属中有大量的自由电子，但是决定金属许多性质的并不是其全部的自由电子，而只是在费米面附近的那一小部分。正因为这样，对金属费米面的了解就显得尤为重要。

该结论推翻了经典电子论的观点，是金属性质研究中最基本最重要的出发点。