固体电子能量理论发展阶段：经典、量子、能带论

经典电子论：代表人物特鲁德（Drude）和洛仑兹，亦称特鲁德模型。

经典电子论的要点：在没有外场作用下，金属中的自由电子沿着各个方向运动的几率相同，故不产生电流。当外加电场后，自由电子定向漂移形成电流，自由电子定向漂移中与正离子发生碰撞，使电子漂移受阻，因而产生电阻。

尽管通过后续学习可知，特鲁德模型具有一定的不完善性，但它依然是一个比较成功的电子理论，时至今日依然是唯象理解金属导电性的有益工具。其中涉及的很多概念也为后续模型所沿用，因此有必要详细阐述个中原理。

1.特鲁德模型对金属结构的解释——葡萄干模型

当金属原子聚集在一起形成金属晶体时，原来孤立原子封闭壳层内的电子（称为芯电子）仍然被紧紧地束缚在原子核附近，芯电子和原子核一起被称为原子实（或离子实）。原子实在三维空间内周期性排布构成晶格。

原来在孤立原子封闭壳层外的电子（称为价电子）由于受到原子核束缚较弱，因此可在金属体内原子实外部空间自由运动。模型示意图如图6-1所示。

从孤立原子结构图中可知，一个原子序数为Za的金属元素原子，有Z 个价电子和和（Za-Z）个芯电子。金属晶体形成后，价电子脱离原子在金属中自由运动，这时亦称它们为传导电子。特鲁德称其为自由电子气系统，可以用经典的分子动力学处理。这是一个很重要的近似，将金属看成是由三维空间中周期性分布的原子实和晶格中自由移动的电子气两部分组成。这一模型也被形象地称为葡萄干模型。

图6-1　孤立原子与金属晶体中的原子结构示意图

2.特鲁德模型的基本假设

（1）自由电子近似：除了电子和原子实的碰撞以外，电子与原子实之间的库仑吸引相互作用完全被忽略（因为带正电的原子实分布均匀）。且因为金属晶体存在表面势垒，电子自由运动的范围仅限于金属内部。当无外加电场时，每个电子做匀速直线运动；当存在外加电场时，每个电子的运动服从牛顿定律。

（2）独立电子近似：忽略电子与电子之间的库仑排斥相互作用，即将金属中的自由电子看作是彼此独立运动的、完全相同的粒子。在独立、自由电子近似中，总能量全部是动能，势能可以被忽略。

（3）碰撞假设：碰撞是运动电子由于撞到不可穿透的原子实而反弹，速度被突然改变的瞬时事件。与理想气体理论不同的是，特鲁德模型忽略了电子之间的碰撞。假设电子和周围环境达到热平衡仅仅是通过碰撞实现的，碰撞前后电子的速度毫无关联，方向随机。则在温度为T 的金属中，把单原子理想气体的内能公式直接用于金属中的电子气体上，得到单个电子的平均能量：

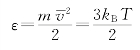
（4）弛豫时间近似。一个电子与原子实发生两次碰撞之间的时间间隔τ称为弛豫时间（或平均自由时间），则单位时间内电子发生碰撞的几率是。它意味着，在任意时刻选定一个电子，在前后两次碰撞之间平均而言，电子将有时间的行程，称为平均自由程l=v0τ。特鲁德进一步假设，弛豫时间与电子位置和速度无关，在无限小的时间间隔dt以内，一个电子碰撞的次数为。(www.xing528.com)

注：值得一提的是，特鲁德模型假定金属电子气类似于理想气体，与声子、光子等同属于玻色子，遵从经典的麦克斯韦-玻尔兹曼统计分布，不遵从泡利不相容原理。这局限了应用特鲁德模型解决问题的范围，也反映了传统统计理论在一些问题面前会遇到困难，故需要进一步发展。

3.特鲁德模型的应用实例

（1）计算出金属的直流电导率，成功解释了欧姆定律。应用特鲁德模型可以推导出直流电流密度j和外电场E 的关系满足j=σE，其中电导率σ=正是欧姆定律。

（2）计算出热导率κ和电导率σ 之间的比例关系，可得到与著名的魏德曼-弗兰兹定律形式一致的公式：

实验证明在常温下是一个普适于所有金属的常数，称为洛伦兹常数。而根据上述公式计算的结果与洛伦兹常数的数量级相同，但还是相差2倍左右。

（3）估算金属电子的弛豫时间和平均自由程，说明特鲁德模型的自洽性。根据能量均分定理以及平均自由程公式结合数量级在10-15～10-14s的弛豫时间τ，可以求得平均自由程在0.1～1nm 范围内，与金属原子间隔一致。这与特鲁德的碰撞假设自洽。

注：在物理学中，理论上的自洽并不等于理论本身是正确的。

4.特鲁德模型遇到的根本性困难

（1）根据经典统计的能量均分定理，N 个价电子的电子气有3N 个自由度，它们对热容的贡献为但对大多数金属，实验值仅为这个理论值的1%，且在低温区与实验不符合。

（2）如上所述，根据模型算出的电子的平均自由程在0.1～1nm 范围内，而实验测得金属的电子平均程在10nm 以上。

（3）经典电子论认为自由电子的顺磁磁化率和温度成比例，但实验证实，自由电子的顺磁磁化率与温度几乎无关。

为解决这些困难，在费米-狄拉克统计理论建立以后，经典电子论发展成为索末菲（Sommerfield）的量子自由电子论。