晶格振动比热容：低温趋近于零

1.晶体比热容的实验规律

（1）在高温时，晶体的比热容为3m NkB，其中N 为晶体中的原胞个数，m 为每个原胞中的原子个数，kB=1.38×10-23J·K-1为玻尔兹曼常量。

（2）在低温时，晶体的比热容按T3趋近于零。

2.晶体比热容的一般理论

固体定容比热容定义为：在物体体积不变的情况下，单位质量的某种物质温度升高1K 所吸收的热量。固体物理中的比热容常用摩尔比热，表达式为

式中：U 为晶体总能量。

晶体的比定容热容由两部分组成：

式中：CV，m（T）声子是晶格摩尔振动比热容；CV，m（T）电子为晶体摩尔电子比热容。

在温度不太低的条件下，CV，m（T）声子≫CV，m（T）电子。本节只讨论晶格振动比热。

（1）高温下晶体的晶格比热容：不考虑量子效应，根据能量均分定理，每一个自由度的平均能量是kBT。若晶体有N 个原胞，每个原胞包含m 个原子，则总自由度为3mN，所以晶体的总能量为

则晶格比热容为

上式表明，在高温条件下，晶格摩尔比热容是一个与材料性质和温度都无关的常数。这就是杜隆-珀蒂定律。但在低温时，经典理论不再适用，必须考虑新的理论。

（2）低温晶格振动的内能（晶格振动的量子理论）：晶体可以看成是一个热力学系统，

在简谐近似下，晶格中原子的热振动可以看成是相互独立的简谐振动。每个谐振子的能量都是量子化的。对于含有N 个原子的三维晶格系统，其总能量为

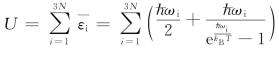
而在运用CV，m=时会遇到求和上的困难。由于频率ω 可以视为准连续的，因此可以将求和变换为积分运算。

为此须引入频谱分布函数——频谱密度或状态函数ρ（ω），表示单位体积的固体中，在ω 到ω+dω 频率间隔内的振动模式数目。且有

因此晶体总能量U 可以写为

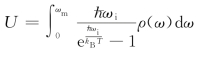
因此晶体摩尔比热容为

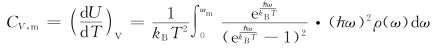
然而对于三维晶体，其频谱密度很难准确求得。因此人们提出了简化模型，较典型的就是爱因斯坦模型和德拜模型。

3.晶体比热的爱因斯坦模型

爱因斯坦模型的假设主要有以下两条：

（1）晶体中原子的振动是相互独立的。

（2）所有原子都具有同一频率ωE，这个频率称为爱因斯坦频率。

设晶体由N 个原子组成，因为每个原子可以沿三个方向振动，共有3N 个频率为ωE的振动。因此晶体总能量为

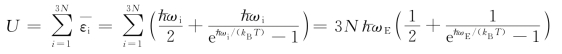
则不难推出，晶体摩尔比热容为

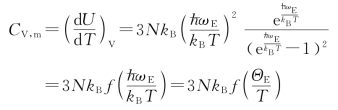
式中：ΘE为爱因斯坦温度。

定义kBΘE=且爱因斯坦比热容函数为

下面讨论爱因斯坦晶格比热理论在高温极限和低温极限下的结果。

1）高温时，ΘE≪T，则爱因斯坦比热函数为

利用ex在x→0时的泰勒展开式为

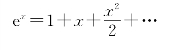
可化简得

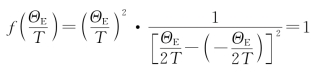
显然，晶体摩尔比热容CV，m=3NkB，符合实验规律。

2）低温时，ΘE≫T，因此

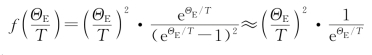
故晶体摩尔比热容：(www.xing528.com)

不难发现，此时CV，m比T3趋于零的速度更快。是什么原因使爱因斯坦模型在低温时不能与实验相吻合呢？根据爱因斯坦温度的定义，爱因斯坦频率ωE大约为1013Hz，处于远红外光频区，相当于长光学波极限。

具体计算表明，在甚低温度下，格波的频率很低，属于长声学波，也就是说，在甚低温度下，晶体的比热容主要由长声学波决定。因此爱因斯坦模型在低温时不能与实验相吻合。

因此，需要采用晶体比热容的德拜模型去解释低温下晶体比热容与温度的关系。

4.格波的总模式密度

频率分布函数：单位体积、单位频率间隔内的振动模式数，大小为

设三维晶体有N 个原子，则有=3N。其求解思路如图4-6所示。

体积元包含的波矢数目为波矢密度与体积元的乘积，即

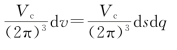
因此，波矢q到q+dq之间的波矢数目为

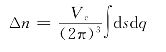
由梯度定义知，dω=|∇qω（q）|dq，代入上式有

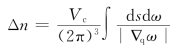
则第α支格波的模式密度为

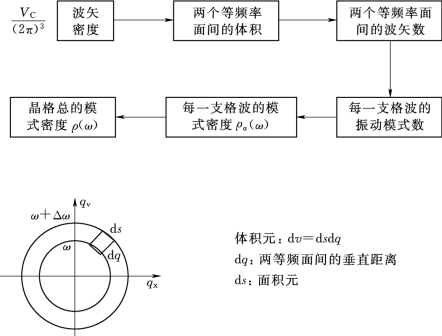
图4-6　求解频率分布函数思路图

将3N 支格波都考虑在内，则格波的总模式密度为

式中：Sα为第α支格波的等频面。

5.晶体比热容的德拜模型

德拜模型的假设主要有以下三条：

（1）假设晶体是各向同性的连续介质，格波为弹性波。

（2）存在一支纵波和两支横波。

（3）晶格振动频率在0～ωD之间，其中ωD为德拜频率。

在波矢空间，等频面Sα是半径为q的球面，因此第α支格波的模式密度为

弹性波有1支纵波、2支横波，共3支格波。所以总的模式密度为

故总模式密度为

不难推出，晶体摩尔比热容为

下面讨论德拜晶格比热理论在高温极限和低温极限下的运用：

（1）高温时，ΘE≤T，x≤1，则德拜比热函数为

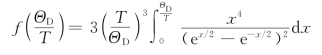
利用ex在x→0时的泰勒展开式：

可求得

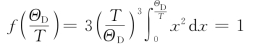
故高温时的晶体比热CV，m=3NkB，显然，高温时与实验规律相吻合。

（2）低温时，ΘE≫T，德拜比热函数：

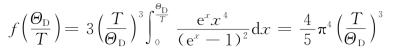
故晶体比热容：

显然，在低温度下，比热与T3成正比，与实验符合。这个规律称为德拜定律。