注:一维单原子链的色散关系推导很重要,读者应理解其思路并能熟练地写出全过程。
1.一维单原子链模型
考虑一系列相同且质量为m 的原子等距地排列在一条无限长的直线上形成一维单原子链(即一维简单晶格)。设在T=0K 下相邻原子在平衡位置间距为r0。由于T>0K 时原子开始不停地热运动,会离开各自的平衡位置,又在近邻原子的作用力下具有返回平衡位置的趋势,从而在平衡位置附近作微振动。弹簧模型可以近似表达这种微振动,如图4-1所示。
图4-1中的第一行表示t=0 的平衡状态下原子链的状态;第二行表示在t时刻,T>0K时各原子偏离平衡位置的状态。xn和xk分别表示第n 个和第k 个原子在t 时刻偏离平衡位置的位移。用xnk=xn-xk表示在t时刻第n 个和第k 个原子间的相对振动位移。

图4-1 一维单原子链模型图
用u(r)表示两个原子间的互作用势能,在T>0K 的t时刻,由于产生相对位移,故引入小量δr→0,则有r=r0+δr。则一维情形下的u(r)的泰勒展开式如下:
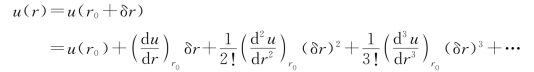
u(r)对自变量r求一次导数并取相反数,可得两原子间的相互作用力f 为
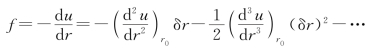
由于振动微弱,根据简谐近似,忽略掉作用力展开式中的非线性项,只保留δr的一次项,故有
![]()
现在考虑第n 个和第k 个原子间的相互作用力fnk。在原子发生微小振动的前提下,可以认为xn、xk和xnk都是位移小量。因此在一维情形下,fnk可以近似写为
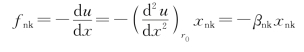
式中:![]() ,称为弹性恢复力系数,很显然对原子间距固定的原子链,βnk是常数,简记为β。因此近邻原子(不一定最近邻)之间的作用都可以近似用一个劲度系数为β的弹簧模型来描述。
,称为弹性恢复力系数,很显然对原子间距固定的原子链,βnk是常数,简记为β。因此近邻原子(不一定最近邻)之间的作用都可以近似用一个劲度系数为β的弹簧模型来描述。
为使问题进一步简化,只考虑最近邻的两个原子对中间原子的相互作用(也称最近邻近似),则第n个原子的振动方程为
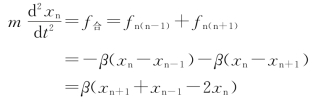
注:在一维三元简谐系统中,中间的球体向任一端运动引起弹簧形变时,两端的球体给中间球体的力的方向均与中间球偏离平衡位置的方向相反,故两个弹力要相加。但这并不是严谨证明,有兴趣的读者可以通过讨论证明。
解上述振动方程,得试探解
![]()
结合第一章中一维布拉菲格子特性可知,一维单原子链的晶格常数a=r0。因此,上述试探解可以写为下列更常用的形式:
![]()
试探解表明,链上原子均以同一角频率ω,同一振幅A振动,任意两原子间的相位差为aq(n′-n),距离为![]() 的整数倍。这说明晶格中各个原子间的振动相互间都存在着固定的位相关系,即原子的振动形成了波,这种波称为格波。在简谐近似下,格波可以分解成许多简谐平面波的线性叠加。
的整数倍。这说明晶格中各个原子间的振动相互间都存在着固定的位相关系,即原子的振动形成了波,这种波称为格波。在简谐近似下,格波可以分解成许多简谐平面波的线性叠加。
将试探解代入原振动方程中,可求得色散关系:
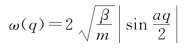
色散关系曲线ω(q)-q如图4-2所示。

图4-2 一维单原子链色散关系曲线
我们发现,色散关系曲线是周期为![]() 的偶函数,且ωm=
的偶函数,且ωm=![]() 由于ω(q)的周期恰为一维简单格子的倒格子原胞长,因此可以将q限制在第一布里渊区内:q∈
由于ω(q)的周期恰为一维简单格子的倒格子原胞长,因此可以将q限制在第一布里渊区内:q∈![]() (只需保证区间一开一闭即可)。
(只需保证区间一开一闭即可)。
这里不妨引入波动力学的两个概念——相速度vp与群速度vg。前者指频率为ω,波矢为q的纯波传播速度;后者指平均频率为ω,波矢为q的波包的速度。对于一维单原子格子,格波的相速度和群速度为
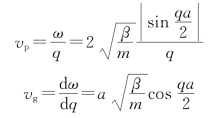
可以看出,格波的相速度、群速度都是波矢q的函数,表明格波具有色散性质。而弹性波的波速只与介质性质有关而与波矢无关。
(1)长波近似(|q|→0):当q取值很小时(λ=![]() 很大),即在布里渊区附近时,色散关系退化为线性关系:(https://www.xing528.com)
很大),即在布里渊区附近时,色散关系退化为线性关系:(https://www.xing528.com)
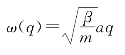
可以进一步得知vp=vg=![]() 符合弹性波的相速度和群速度关系。这是因为在格波波长很大时,晶格常数a相比之下显得很小,所以晶格被看作连续介质,故此时格波接近于连续介质中的弹性波,波速与波矢q无关。一般也称单原子链中传播的长格波为声学波。
符合弹性波的相速度和群速度关系。这是因为在格波波长很大时,晶格常数a相比之下显得很小,所以晶格被看作连续介质,故此时格波接近于连续介质中的弹性波,波速与波矢q无关。一般也称单原子链中传播的长格波为声学波。

注:一维单原子链的色散关系与长波、短波近似本身就可以命制一道大题,因此务必熟练掌握。
2.一维双原子链模型
在一维单原子链的基础上,我们研究一维无限长双原子链。不妨设其包含N 个原胞,则共有2N 个原子,两种原子的质量分别为m 和M,且m<M。晶格常数为a,相邻原子间距为![]() 恢复力系数为β。同样原子只能沿直线的两个方向振动。如图4-3所示。
恢复力系数为β。同样原子只能沿直线的两个方向振动。如图4-3所示。
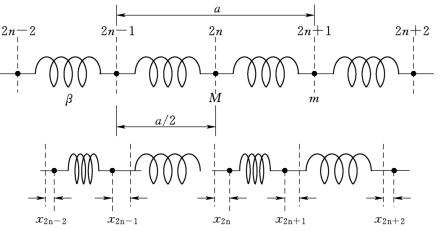
图4-3 一维双原子链模型图
易写出振动方程
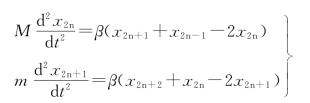
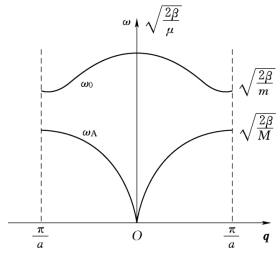
图4-4 一维双原子链色散关系曲线
中间求试探解再代入的步骤不再赘述。可以解得色散关系为

很显然,一维双原子链的ω 和q 之间存在两种不同的色散关系。其中频率ω0的取值较高,称为光学模,其对应的格波可以用光激发,故称为光学支格波;频率ωA的取值较低,称为声学模,其对应的格波称为声学支格波。
从图4-4中看出,当q取±![]() 时,光学波与声学波之间存在一个频率间隙,即ω 不能在这个间隙中取值。频率间隙也是能量间隙,对应于声子能量的禁带。两原子质量差别越大,光学波和声学波之间的频隙就越宽,而光学波本身的频率范围也就越窄。
时,光学波与声学波之间存在一个频率间隙,即ω 不能在这个间隙中取值。频率间隙也是能量间隙,对应于声子能量的禁带。两原子质量差别越大,光学波和声学波之间的频隙就越宽,而光学波本身的频率范围也就越窄。
长声学波:相邻原子的位移相同,原胞内的不同原子以相同的振幅和位相作整体运动。因此,可以说,长声学波代表了原胞质心的运动。不难证明,|q|→0 时,声学模![]() 因此该支格波的相速度等于群速度,是声学支。
因此该支格波的相速度等于群速度,是声学支。
长光学波:原胞的质心保持不动,两相邻原子振动方向相反。所以定性地说,长光学波代表原胞中两个原子的相对振动。
长声学波与长光学波的区别如图4-5所示。
3.玻恩-卡门假设及主要结果
前面推出的振动方程,仅适用于无限长原子链,而实际晶格是有限的。为使在无限长原子链上推出的振动方程适用于有限长的晶体,玻恩和卡门把边界对内部原子振动状态的影响考虑成如下所述的边界条件:
(1)由M 个原子构成的原子链,为无限长原子链中的一段,且M=m N,其中N 为原胞数,m 为每个原胞中的原子数;
(2)把这M 个原子组成的一维原子链看成一个闭合环,它包含有限数目的原子,但实际上第(M+1)个原子就是第一个原子。
只要N 足够大,圆环半径远大于晶格常数a,就局部看来,仍可认为原子排列在一条直线上。周期性边界条件既保证了原子数的有限,又消除了边界的影响,简化了方程的求解。从而可推出如下结论(表4-1):
1)晶格振动的波矢数=晶体中的原胞数。
2)晶格振动频率数=晶体中所有原子的自由度数。
3)晶格振动模式数=晶体中所有原子的自由度数。
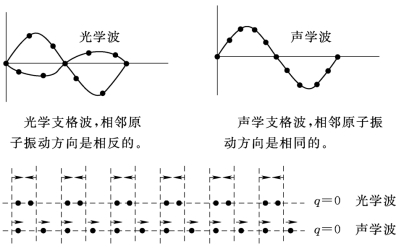
图4-5 一维双原子链中长声学波与长光学波的区别
表4-1 典型晶体中波矢数与频率数
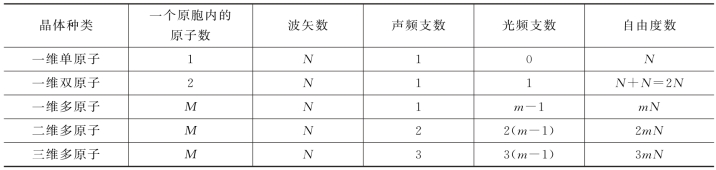
注 表4-1可以适当理解记忆,有利于快速解题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




