1.布拉格反射公式
(1)X 射线的特性:波长短,穿透力强,适用于研究物质结构。但随之而来的缺点是,当X 射线入射到光滑的固体表面时,所有材料对其折射率几乎都为1,也就是说X 射线的透射率极大而反射率极小,造成反射光束较弱。
(2)布拉格公式的推导:布拉格依据光的干涉理论提出一个简单的设想。单色X 光入射晶体中的原子平面并镜面反射。虽然反射波仅为入射波的10-3~10-5,但由于X 光穿透能力强,就有足够多的原子平面参与反射。也就是说,可以将晶体看作一组与晶体表面平行的等劳厄间距的镜面。
另一方面,由于X 射线的波长与晶体中一组平行原子平面的面间距相当,因此当反射光发生相长干涉时,就能获得足够强的衍射光束,如图2-1所示。
在此衍射过程中,只要认为入射粒子和出射粒子能量基本相同,就可以认为是弹性散射过程。因此,X 射线的波长在反射前后保持不变,即λ=![]()
从图2-1中可以得知,相邻平面的反射光光程差为2dsinθ。当光程差是X 射线波长λ的整数倍时,就可以发生相长干涉,即有
![]()
这就是布拉格公式,其中n是衍射级数,反映同一晶面族在不同入射角下的衍射,取正整数。本质上是点阵周期性所导致的结果。
(3)布拉格公式的运用:布拉格公式反映出晶面族对波长一定的X 射线能否反射具有选择性。只有入射角满足布拉格公式,才能在按照反射定律的方向上观察到衍射。
(4)局限性:布拉格公式只能给出衍射加强的条件,却不能给出衍射强度的分布。其物理模型过于简单,也忽略了晶面上原子的分布及种类对衍射的影响。
2.劳厄方程
(1)坐标空间的劳厄方程:如图2-2所示,在简单布拉菲格子中取格点O 为原点,则任一格点A的位矢为
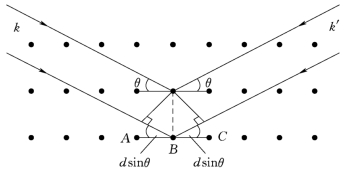
图2-1 布拉格衍射
![]()
设s0和s分别为入射线和衍射线方向上的单位矢量,则光程差
![]()
因此对单色X 射线而言,衍射加强条件为
![]()
(2)倒易空间的劳厄方程:由于倒易空间的一个阵点就与正格子的一族晶面相对应,所以研究倒易空间的劳厄方程更有意义。
在坐标空间中,s0和s分别为入射线和衍射线方向上的单位矢量。则在倒易空间中入射线与衍射线方向对应的矢量为(https://www.xing528.com)
![]()

图2-2 坐标空间下的X 射线衍射
代入Rl·(s-s0)=μλ,化简得
![]()
而(k-k0)必为倒易空间的位置矢量,即
![]()
与布拉格公式类似,n 为正整数,称为衍射级数,(h1h2h3)是晶面指数,而(nh1,nh2,nh3)称为衍射面指数。该方程与坐标空间的劳厄方程是等价的,决定了出现衍射极大方向的条件,故也称为劳厄条件。其意义为:在与入射波矢相差一个或几个倒格矢的衍射波矢方向上,将出现衍射极大。
值得一提的是,由劳厄方程可以直接推导布拉格反射公式。得出结论:当衍射线对于某一晶面族来说恰好是光的反射方向时,此衍射方向就是衍射加强方向。
3.X 射线衍射的实验方法
注:这部分实验性较强,在材料测试分析相关课程中会着重教授。
(1)辅助工具——厄瓦德球:在倒空间内取一结点为原点O,以入射波矢k 的始端C为球心、终端落在O 上,并以|k|=![]() 为半径画一个球,如图2-3所示。
为半径画一个球,如图2-3所示。
(2)常用的三种方法:劳厄法、旋转单晶法、粉末法(德拜法)。在此不再赘述。
4.原子散射因子与几何结构因子
劳厄方程或布拉格方程仅考虑了晶格格点的周期性排列所产生的结果,但并没有涉及组成晶体的原子和原胞的具体性质。当点阵基元中原子的种类不同时,要考虑不同原子对X射线的散射作用——原子散射因子;当点阵中的原胞内原子分布不同,还要考虑原胞中不同位置的原子对X射线的散射作用——几何结构因子。
原子散射因子的定义:原子内所有电子在某一方向上引起的散射波的振幅的几何和,与某电子在该方向上引起的散射波的振幅之比。
几何结构因子的定义:原胞内所有原子在某一方向上引起的散射波的振幅的几何和,与某个原子在该方向上引起的散射波的振幅之比。
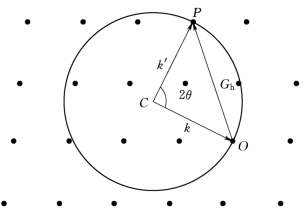
图2-3 厄瓦德球构造示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




