【摘要】：一个晶体的对称操作数目越多，其对称性越高。因此，常用对称群来描述晶体的性质。由于晶体的所有宏观对称操作都不改变一个特殊点的位置，常称宏观对称性为晶体的点群，晶体点群有32种。用这8种独立的对称操作任意组合，构成32种不重复的组合操作。这是晶体可以分为32个点群的直接依据。
1.对称操作
一个晶体在经某一变换后，晶格中格点在空间的分布保持不变，这一变换称为对称操作。一个晶体的对称操作数目越多，其对称性越高。
对称操作分为两类：平移对称操作和点对称操作。
2.点群对称操作的性质
（1）必须具有不变操作。
（2）如果具有两个对称操作A和B，则这两个相继连续操作的组合仍为一个对称操作。
（3）如果A为对称操作，其逆操作也是对称操作。
（4）如果A、B、C为对称操作，则先操作C 后A与B的组合与先操作B 与C 的组合再操作A的效果一致。
这些性质与数学中群的性质相符。因此，常用对称群来描述晶体的性质。由于晶体的所有宏观对称操作都不改变一个特殊点的位置，常称宏观对称性为晶体的点群，晶体点群有32种。
3.独立的对称操作(www.xing528.com)
独立的对称操作共有如下8种：
5种旋转对称操作：1、2、3、4、6度旋转对称操作，常用C1、C2、C3、C4、C6表示。
中心反映（1种）：用i表示。
镜像反映（1种）：用m 表示。
4度旋转反演轴（1种）：用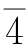
或S4表示。
用这8种独立的对称操作任意组合，构成32种不重复的组合操作。这是晶体可以分为32个点群的直接依据。
4.n度螺旋轴和滑移反映面
独立对称操作加上n 度螺旋轴和滑移反映面组成230种空间群。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
