中国碳市场调查：市场价格波动特征实证检验结果

1.GARCH模型的原理

我国7个碳排放权交易试点的市场价格波动具有随时间变化的特征，有时相当稳定，有时波动异常激烈，变化呈现波动集群性，即在整个序列观察期，序列的方差是齐性的，但在某一段或者某几段时期的方差却显著异于期望方差。这种波动聚集现象，通常出现在宏观经济和金融领域的时间序列上。针对这种现象，目前常用的办法就是构建自回归条件异方差模型（ARCH），此模型是计量经济学家恩格尔20世纪80年代提出的，并成功地应用于英国通货指数的波动性研究。很多学者从不同角度推广了ARCH模型，进一步拓展了ARCH模型的应用领域，例如广义自回归条件异方差模型（GARCH）。GARCH模型是在ARCH模型的基础上，增加了异方差函数的p阶自相关而形成的，它可以有效地拟合具有长期记忆性的异方差函数。ARCH族模型能模拟时间序列变量的波动性变化，它在计量金融领域中应用较为广泛。我国的碳排放权交易市场由于成立的时间较短，还不太完善，那么价格波动是否具有这些特征呢？我们通过建立GARCH模型对我国7个试点省市碳排放权交易价格的分布特征及波动状况进行研究。显然，研究这一问题对我国构建稳定的碳排放权交易市场具有重要的指导意义。

2.GARCH模型

（1）ARCH模型结构为：

为了条件方差ht＞0，残差平方序列平稳，要求：

式（4.1）中，f（t，yt-1，yt-2，…）为确定性信息拟合模型，yt为被解释变量，yt-1，yt-2…为滞后期变量，μt为随机扰动项，μt～N（0，ht）。式（4.2）中系数ti＞0（i=0，1，2，…，q），ht是通过历史信息采用某种自回归形式刻画波动的变化。

（2）GARCH模型的基本形式：

在ARCH模型中，当εt的条件方差需要依赖于很多点之前的滞后项，则必须估计大量参数，在实际操作中往往难以做到。因此，波勒斯勒夫（1986）提出使用少量的滞后项代替大量的滞后项，构建GARCH模型（广义自回归条件异方差）。GARCH（p，q）模型的均值方程与ARCH（q）模型无异，但在条件方差方程中将的条件方差表示为：

其中，p为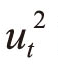的滞后项阶数，，表示1至p阶滞后项，θ1，…，θp为这些滞后项的回归系数；此外，p≥0，q＞0；α0＞0，αi≥0，i=1，…，q；θj≥0，j=1，…，p； 。

3.试点碳市场价格波动率的描述分析

由于重庆交易所碳排放成交量低迷，故未对其进行分析，我们选取6个试点市场从交易初期到2016年8月12日有交易记录的数据。采用价格波动率指标度量价格的波动特征，为了得到平稳的价格波动时间序列数据，采用取自然对数方法进行分析，价格波动率的计算公式为：

式（4.4）中，Pt和Pt-1分别是第t和t-1时期碳排放权交易市场价格，Rt为价格波动率。6个碳试点的价格波动率如表4-1所示。

表4-1　碳交易市场价格波动率描述分析

从价格波动率均值上看，其刻画了价格波动率的平均程度，数值越大说明价格的波动越大。从表4-1可以看出，各个碳排放权交易市场的价格波动率都比较低，其中北京的最低，说明各个市场的价格波动并不剧烈。从偏度、峰度和J-B统计量可以看出，各个碳排放权交易市场价格波动率分布都不是正态分布，具有尖峰、后尾的特征。

4.碳市场价格波动率平稳性检验

在建立模型过程中，不能直接用非平稳的变量序列进行，所以在进行分析前，要先对序列进行平稳性检验。本书采用ADF检验方法，结果表4-2所示。

表4-2　价格波动率序列ADF检验结果

结果表明：6个碳交易市场的价格波动率序列均拒绝原假设，说明序列不存在单位根，表明序列平稳。(www.xing528.com)

5.市场价格波动特征的实证检验

（1）构建AR模型。由于要对多个市场构建GARCH模型，采用的步骤和方法基本相同，所以先以湖北市场为例确定主要步骤。从上文构建量价结合的模型可知，价格作为因变量，其一阶滞后项作为自变量，得到的自变量回归系数均显著，初步验证了t-1期的流动性对t期流动性有影响，所以我们建立如下的AR（1）模型（一阶自回归）：

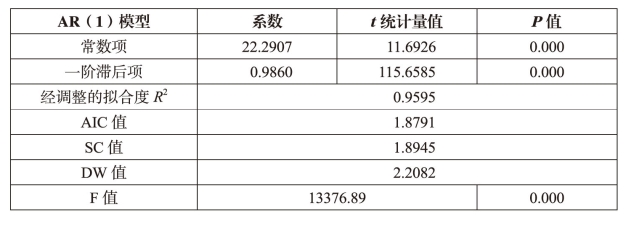
其中，t代表研究时间区间内t个交易日，Rt表示在第t个交易日的价格波动率，Rt-1表示价格波动率的一阶滞后项；β0为常数项，β1为一阶滞后项的自回归系数，εt为残差。我们运用EVIEWS软件建立上述AR（1）模型。表4-3给出了模型的输出结果，模型中一阶滞后项为0.986，且在0.01水平上显著。此外，模型调整后的拟合度R2为0.96，可见，AR（1）模型有力地验证了t-1期流动性对t 期流动性的正向作用。

表4-3　湖北碳市场价格波动率AR（1）模型输出结果

以上述AR（1）模型的残差εt作为研究对象，描绘出它的时间序列图形，如图4-1所示。可见，模型的残差εt均在发生较大幅度波动后继续发生较大幅度波动，而在发生较小波动后继续发生较小幅度的波动，即具有“波动集聚性”（Volatility Clustering）。

（2）ARCH效应检验。为了建立GARCH模型，首先运用EVIEWS软件提供的LM检验（拉格朗日乘数）分析湖北碳市场价格波动率AR（1）模型的残差εt是否存在显著的ARCH效应，即检验回归系数是否同时为0。检验结果表明，F统计量和T×R2统计量分别为7.6142、7.5525，P值分别为0.0060、0.0060，两个统计量均在0.01水平上显著，拒绝不存在ARCH效应的原假设，说明湖北碳市场价格波动率AR（1）模型的残差εt存在显著的ARCH效应。

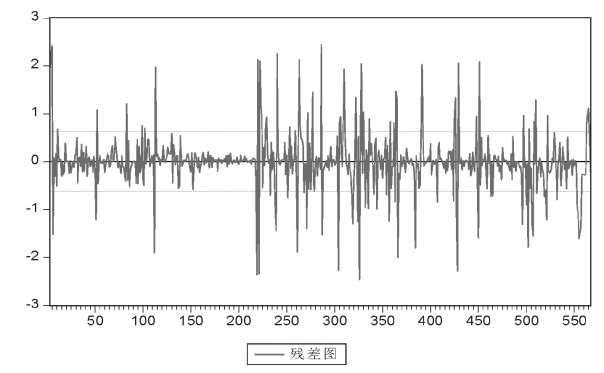
图4-1　AR（1）序列残差图

（3）GARCH模型的构建。针对湖北碳市场价格波动率，我们建立以下GARCH（1，1）模型：

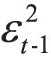其中，均值方程等式左边的Rt表示第t个交易日的价格波动率，等式右边的Rt-1表示价格波动率的一阶滞后项；β0为常数项，β1为一阶滞后项的回归系数，εt为残差。条件方差方程等式左边的为εt的条件方差，等式右边的为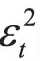的一阶滞后项，被称为ARCH（1）项为的一阶滞后项，被称为GARCH（1）项；α0为常数项，α1为ARCH（1）项的回归系数，θ1为GARCH（1）项的回归系数；此外，要求α1+β1＜1。

（4）GARCH模型结果。本文运用EVIEWS软件估计湖北碳市场价格波动率GARCH（1，1）模型，模型结果如表4-4所示。

表4-4　湖北碳市场价格波动率GARCH（1，1）模型

续表

在均值方程中，模型常数项和一阶滞后项系数都为正，且在0.01水平上显著，表明前期价格波动率对当期的价格波动率存在正向作用。

在条件方差方程中，ARCH（1）项和GARCH（1，1）项的回归系数均为正，且在0.01水平上显著。GARCH方程中α1+θ1接近于1，表明条件方差函数具有单位根和单整性，也就是说条件方差波动具有持续记忆性，说明湖北碳市场价格波动率对外部冲击的反应以一个相对较慢的速度递减，并且模型的ARCH（1）项和GARCH（1）项的回归系数之和小于1，这与预期不符。

模型的经调整的拟合度R2略小于AR（1）模型，AIC值和SC值均低于前面的AR（1）模型。可见GARCH（1，1）模型可以较好地描述湖北碳市场价格波动率的变化，特别是表现了价格波动率的波动集聚性，即价格波动率变化的条件方差所受到的冲击具有较强的持久性。

湖北碳市场价格波动最终拟合的模型表达式为：