高等数学应用基础复习题及解答

一、填空题

1.方程的解为_____.

2.方程组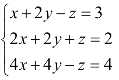的解为=_____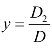，=_____，=_____.（用行列式表示方程组的解）.

3.行列式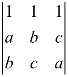=__________（利用对角线法则展开）；

行列式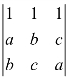=__________（按第一行展开）.

4.若行列式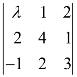中，4 的代数余子式 A22=-1，则λ=_____.

5.行列式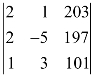的值是_____.

6.设矩阵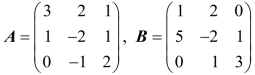，故A+B=_____，A-B=_____，AB=_____，BA=_____.

7.矩阵的秩为_____；矩阵（1 2 3）的秩为_____.

8.AA-1=______.

9.若三阶方阵A 可逆，则 r（A）=_____.

10.已知四元齐次线性方程组AX=0 有非零解，故 r（A）可能等于_____.

二、判断题

1..（ ）

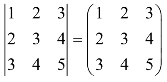2.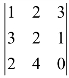中，4 的代数余子式为.（ ）

3..（ ）

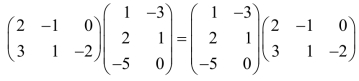4.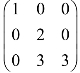是行阶梯形矩阵.（ ）

5.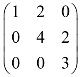是满秩矩阵.（ ）

6.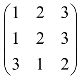不可逆.（ ）

7.任何一个线性方程组都可以用克莱姆法则来求解.（ ）

8.方程组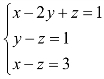无解.（ ）

三、选择题

1.下列运算结果是3 行4 列矩阵的是（ ）.

A.A3×2 B2×2 B.A3×2 B2×4 C.A3×4 B4×2 D.A2×2 B2×3

2.对于同阶方阵A，B，C，下列运算正确的是（ ）.

A.AB=BA B.A(B+C)=AB+AC

C.(A+B)(A-B)=A2-B2 D.(A-B)2=A2-2AB+B2

3.下列矩阵中，秩为3 的是（ ）.

A. B.

C.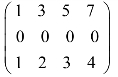 D.(1 2 3)

4.若非齐次线性方程组AX＝b 的增广矩阵B 经过初等行变换变为

则方程组的解的情况为（ ）.

A.无解 B.唯一解

C.无穷多解 D.有限个解

5.若齐次线性方程组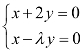有非零解，则λ=（ ）.

A.2 B.1 C.-2 D.-1

6.已知方程组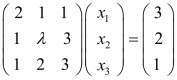无解，则λ=（ ）.(www.xing528.com)

A.2 B.1 C.-2 D.-1

7.n 元线性方程组AX=0 有非零解的充要条件是（ ）.

A.方程个数m＜n B.方程个数m＝n

C.方程个数m＞n D.秩 r（A）＜n

四、解答题

1.计算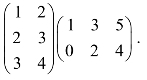

2.已知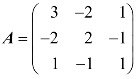，求A-1.

3.已知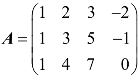，求 r（A）.

4.解方程组：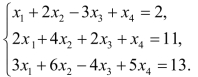

5.解方程组：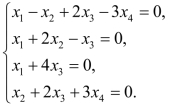

6.解方程组：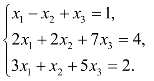

【阅读材料】

浅谈线性代数

1.什么是线性代数

线性代数是数学的一个分支，它是研究线性问题的代数理论.那么什么是代数呢？

代数的英文名称是Algebra，源于阿拉伯语，其本意是“结合在一起”的意思.也就是说，代数的功能是把许多看似不相关的事物“结合在一起”，也就是进行抽象，抽象的目的是提高解决问题的效率.比如，线性代数中一个重要的抽象概念是线性空间（满足“加法”和“数乘”等八条公理的元素的集合），而其元素被称为向量.也就是说，只要集合里的元素满足公理，元素之间的变化满足这些规律，我们就可以对这个集合（即线性空间）进行一系列的线性化处理和分析，而关于这个陌生的集合的性质和结构，我们一下子就全知道了，这就是代数的一个抽象特性.既然这个具有特性的集合叫线性空间，顾名思义，当然具有直观的几何意义.线性来源于直线的几何概念，空间来源于二维平面或三维空间的几何概念.所有类型的线性空间都和直线、平面、三维立体以及高维正交空间的变换性质一样，所有类型的线性空间里的元素都可以和线性空间的点（向量）相互对应.

线性代数的研究对象是向量、向量空间（或线性空间）、线性变换和有限维的线性方程组.线性代数更是讨论矩阵理论、与矩阵结合的向量空间及其线性变换理论的一门学科.向量空间是现代数学的一个重要课题，因而线性代数被广泛地应用于抽象代数和泛函分析中，并且通过解析几何，使其得以被具体表示.线性代数的理论已被泛化为算子理论.科学研究中的非线性模型通常可以被近似为线性模型，这使得线性代数被广泛地应用于自然科学和社会科学中.线性代数主要分为向量、行列式、矩阵、线性方程组几大板块.

2.线性代数的发展历史

线性代数起源于二维和三维直角坐标系的研究.在这里，一个向量是一个有方向的线段，由长度和方向同时表示，这样向量就可以用来表示物理量.现代线性代数已扩展到任意或无限维空间，一个维数为n 的向量空间叫n 维空间，在二维和三维空间中大多数结论已扩展到高维空间.尽管许多人不容易想象n 维空间里的向量，但是实际上用这样的向量（即n 元组）来表示数据却是非常有效的.作为n 元数组，向量是n 个元素的“有序”列表，大多数人可以在这种框架中有效地概括和分析数据.由于费马和笛卡尔的工作，现在一般认为线性代数出现于17世纪，18世纪末，线性代数领域的研究还只限于平面与空间，只是到了19世纪上半叶才完成了向n 维向量空间的过渡.矩阵论始于凯莱，在19世纪下半叶才达到了它的顶点.1888年，皮亚诺以公理的方式定义了有限维或无限维向量空间.托普利茨将线性代数的主要定理推广到任意体上最一般的向量空间中.

3.线性代数被广泛应用的原因

第一、大自然的许多现象是线性变化的，使得人们对单个变量之间的关系进行研究.例如，物理学科中，机械运动的基本方程是牛顿第二定律，即物体运动的加速度与它所受到的外力成正比，其实这又恰恰符合基本的线性微分方程.

第二、随着科学的发展，我们不仅要研究单个变量之间的关系，还要进一步研究多个变量之间的关系，因为各种实际问题在大多数情况下可以线性化，而且随着计算机的发展，线性化了的问题又可以计算出来，所以线性代数成为解决这些问题的有力工具而被广泛应用.

第三、在数学中，几何和代数有着不可分割的联系.线性代数所体现的几何观念与代数方法之间的联系，使人们从具体的概念中抽象出公理化方法，这对于强化人们的数学训练，增强科学性是非常有用的.

4.线性代数在日常生活中的应用

以减肥配方为例.

现在，大学生在饮食方面存在很多问题，多数大学生不重视早餐，日常饮食也没有规律，因此，为了身体健康，大学生应注意日常饮食中的营养.大学生每天的配餐中需要摄入一定的蛋白质、脂肪和碳水化合物，下表给出了三种食物提供的营养以及大学生正常生活所需要的营养（它们的质量以适当的单位计量）.

设三种食物每100 g 中蛋白质、脂肪和碳水化合物的含量如下表所示，表中还给出20世纪80年代美国流行的剑桥大学医学院的简洁营养处方.现在的问题是：如果用这三种食物作为每天的主要食物，那么它们的用量应各取多少，才能实现这个营养要求？

设脱脂牛奶用量为 x1 个单位（100 g），大豆面粉的用量为 x2个单位（100 g），乳清的用量为 x3 个单位（100 g），表中的三个营养成分列向量为：

则它们的组合所具有的营养为

使这个合成的营养与剑桥大学的配方要求相等，就可以得到以下矩阵方程：

解这个矩阵方程得

即脱脂牛奶的用量为27.7 g，大豆面粉的用量为39.2 g，乳清的用量为23.3 g，就能保证所需的综合营养量.

5.线性代数在其他领域的应用

建筑工程方面，奥运场馆鸟巢的受力分析需要线性代数工具；石油勘探方面，勘探设备获得的大量数据所满足的几千个方程组需要线性代数的知识来解决；气象方面，为了做天气预报，有时往往根据诸多因素最后归结为解线性方程组；国民经济方面，为了预测经济形势，利用投入产出经济数学模型，也往往归结为解一个线性方程组.

综上所述，线性代数已渗入到我们生活和工作的方方面面，在未来，线性代数在计算机图形、计算机辅助设计中将发挥更大的作用.它会改变我们的生活，带我们进入一个奇妙的世界.