1.已知数据表1：
表1
（1）预测x=5时，y 的值；
（2）估计x=1.5时，y 的值.
2.在12 h 内，从0 点开始，每隔1 h 测量一次温度，温度依次为5，8，9，15，25，31，30，22，25，27，24，28，试估计在3.5，6.5，7.2，11.3 h 时的温度.
3.在某项试验中，测得的数据如表2 所示：
表2
试求：（1）y 与x 的回归直线方程；
（2）当x=5.61时，估算y 的值.
4.一种物质吸附另一种物质的能力与温度有关，现测试在不同温度下的吸附量，测试结果如表3 所示，试求吸附量y 关于温度x 的一元回归方程.
表3
5.有一组滑轮，要用力F（N）举起质量为W（kg）的物体，实验数据如表4 所示，求适合上述关系的经验公式.
表4
【阅读材料】(www.xing528.com)
数学建模简介
在科学技术发展的过程中，人们用建立数学模型的办法解决了需要寻求数量规律的现实问题，也取得了很多成果.数学建模是联系数学和实际问题的桥梁，是数学在各个领域广泛应用的具体实现.在计算机技术迅速发展的今天，计算机技术成为计算和建模数学向科学技术转化的主要途径.现在，数学建模在科学技术发展中的重要作用受到人们的普遍重视，成为现代科技工作者必备的重要能力之一.
数值计算主要是研究用计算机求解各种数学问题的计算方法及其理论与软件实现.用计算机解决实际问题有几个主要过程：（1）实际问题；（2）数学模型；（3）数值计算方法；（4）程序设计；（5）上机计算求出结果.
数学建模本身不是新东西，它几乎是一切应用科学的基础.古今中外，凡是要用数学来解决的实际问题，几乎都是通过数学建模这一过程来解决的.20世纪以来，科学技术得到飞速发展，数学在这个发展过程中发挥了不可替代的作用.同时，由于计算机的迅速发展和普及，大大增强了用数学解决现实问题的能力，数学模型这个词汇也越来越多地出现在现代人的生活、工作和社会活动中.如天气预报数学模型、交通控制数学模型，等等.模型是客观事物的一种简化的表示和体现，如飞机模型、建筑模型等.那么，什么是数学模型呢？简言之，就是通过抽象和化简，使用数学的语言，对实际问题的一个近似描述，以便人们更深刻地认识所研究的对象.可以说，数学模型是数学与实际问题之间的一座桥梁.数学模型具有三个特征：实践性；应用性；综合性.数学建模的过程就是建立数学模型来解决各种实际问题的过程.
初等数学建模实例
一房地产公司有50 套公寓要出租.当租金定为每套每月1800 元时，公寓会全部租出去，当租金每月增加100 元时，就有一套公寓租不出去，而租出去的房子每月需花费200 元的整修维护费.
（1）建立总收入与租金之间的数学模型.
（2）当房租定为多少时可获得最大收入？
解：（1）建立数学模型.
设租金x 元/月，租出去的公寓有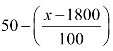
套，总收入为R，所以
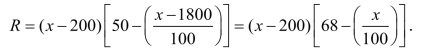
（2）问题归结为：当x 为多少时，R 取最大值.
将上式两边对x 求导得
则x=3500（元/月）.
R（x）只有一个驻点，且为极大值点，也为最大值点.这时总收入为：R（350）=105 600 元.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
