一、填空题
1.总体 X~N(20,3)的容量分别为10,15 的两个独立样本的均值差X-Y~________.
2.设X1,X2,…,X16为取自总体X~N(0,0.52)的一个样本,若已知χ02.01(16)=32.0,则 =________.
=________.
3.设总体X~N(μ,σ2),若μ 和σ2均未知,n 为样本容量,总体均值μ 的置信水平为1-α的置信区间为![]() ,则λ 的值为________.
,则λ 的值为________.
4.设X1,X2,…,Xn为取自总体X~N(μ,σ2)的一个样本,对于给定的显著性水平α,已知关于σ2检验的拒绝域为χ2≤χ12-α(n-1),则相应的备择假设H1为________.
5.设总体X~N(μ,σ2),σ2已知,在显著性水平0.05 下,检验假设H0:μ≥μ0,H1:μ<μ0,拒绝域是________.
二、选择题
1.设X1,X2,X3是取自总体X 的一个样本,α 是未知参数,以下函数是统计量的为( ).
A.α(X1+X2+X3) B.X1+X2+X3
C.![]() D.
D.
2.设X1,X2,…,Xn为取自总体X~N(μ,σ2)的样本, 为样本均值,
为样本均值,![]() 则服从自由度为n-1的t 分布的统计量为( ).
则服从自由度为n-1的t 分布的统计量为( ).
A.![]() B.
B.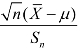
C.![]() D.
D.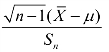
3.设 X1,X2,…,Xn是来自总体的样本,D(X)=σ2存在,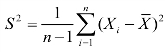 ,则( ).
,则( ).
A.S2是σ2的矩估计 B.S2是σ2的极大似然估计
C.S2是σ2的无偏估计和相合估计 D.S2作为σ2的估计,其优良性与分布有关
4.设总体X~N(μ1,σ12),Y~N(μ2,σ22)相互独立,样本容量分别为 n1,n2,样本方差分别为 S12,S22,在显著性水平α 下,检验H0:σ12≥σ22,H1:σ12<σ22的拒绝域为( ).
A.![]() B.
B.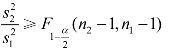
C.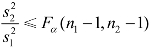 D.
D.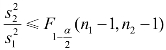
5.设总体X~N(μ,σ2),σ2已知,μ 未知,x1,x2,…,xn是来自总体的样本观察值,已知μ 的置信水平为 0.95 的置信区间为(4.71,5.69),则取显著性水平α=0.05时,检验假设H0:μ=5.0,H1:μ≠5.0的结果是( ).
A.不能确定 B.接受H0
C.拒绝H0 D.条件不足,无法检验
三、解答题
1.设随机变量X 的概率密度为:(https://www.xing528.com)
其中未知参数θ>0,X1,…,Xn是来自X 的样本,求(1)θ 的矩估计;(2)θ 的极大似然估计.
2.设总体X~N(0,σ2),且 x1,x2,…,x10是样本观察值,样本方差 s2=2,
(1)求σ2的置信水平为0.95 的置信区间;
(2)已知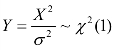 ,求
,求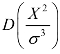 的置信水平为0.95 的置信区间.(
的置信水平为0.95 的置信区间.(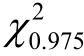 (9)=2.70,
(9)=2.70,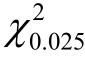 (9)=19.023)
(9)=19.023)
3.设总体X 服从参数为θ 的指数分布,其中θ>0未知,X1,…,Xn为取自总体X 的样本,若已知![]() ,求:
,求:
(1)θ 的置信水平为1-α 的单侧置信下限;
(2)某种元件的寿命(单位:h)服从上述指数分布,现从中抽得容量为16 的样本,测得样本均值为5010 h,试求元件的平均寿命的置信水平为0.90 的单侧置信下限.(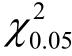 (31)=44.985,
(31)=44.985,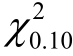 (32)=42.585).
(32)=42.585).
4.某工厂正常生产时,排出的污水中动植物油的浓度 X~N(10,1).现阶段性地抽取 10个水样,测得平均浓度为10.8 mg/L,标准差为1.2 mg/L,问该工厂的生产是否正常?(α=0.05,t0.025(9)=2.2622,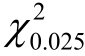 (9)=19.023,
(9)=19.023,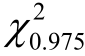 (9)=2.700)
(9)=2.700)
5.设X1,X2,X3,X4为取自总体X~N(μ,42)的样本,对假设检验问题H0:μ=5,H1:μ≠5,
(1)在显著性水平0.05 下求拒绝域;
(2)若μ=6,求上述检验所犯的第二类错误的概率β.
6.设随机变量X 服从自由度为(m,n)的F 分布,
(1)证明:随机变量![]() 服从自由度为(n,m)的F 分布;
服从自由度为(n,m)的F 分布;
(2)若m=n,且 P{ X>α}=0.05,求![]() 的值.
的值.
【阅读材料】
近代统计学之父——凯特勒
数理统计学派的创始人是比利时的数学家、天文学家和统计学家凯特勒(1796—1874).凯特勒出身于比利时甘特市的一个小商人家庭,他对数学有着特殊的爱好,对统计学有着巨大贡献.他在其代表作《概率论书简》《统计学研究》中,将概率论和统计方法引入社会经济方面的研究,他认为,统计学是一门既研究社会现象又研究自然现象的方法论科学.他也因此被尊称为“近代统计学之父”.
人类的统计实践活动其实在原始社会就有了.自文艺复兴以后,人们就注意到,诸如玩纸牌、掷骰子的赌博活动,在大量进行之后,会有某种类型的规律出现.凯特勒在其研究中发现,以往被人们认为从个体来说具有偶然性、从整体来说是杂乱无章的社会犯罪现象,同样也具有一定的规律性.他认为,统计学不仅要反映各国的国情,要研究社会现象,而且还要研究社会现象背后的这种规律性,他还认为,社会现象背后的这种规律性是社会内部固有的,而不是“神定秩序”,人们可以通过计算统计指标来揭示这些规律.凯特勒的这一思想为近代统计学的科学化奠定了基础,也给后世统计学家以深刻的影响.
凯特勒不顾当时统治阶级常有的偏见,从实际出发,提出犯罪和贫穷之间并不存在必然联系.他根据统计资料得出结论:鉴于最贫穷地区的犯罪数目不及经济发达地区的犯罪数目大,犯罪反而与富裕有关.在凯特勒的工作中处处闪烁着社会统计规律性思想的光辉,这给后人以极大的启迪.
凯特勒在自己的研究工作中,把统计学的方法引入到天文学、气象学、地理学、动物学、植物学等自然科学领域.他的这种数理统计方法是应用于任何事物数量研究的最一般方法,对以后统计学的发展具有重大意义.
凯特勒是当时统计学界的中心人物.他担任过比利时中央统计局局长,主持过第一次国际统计会议(1853年);他最先将概率论应用于人口、人体测量和犯罪等问题的研究中,从而完成了统计学和概率论的结合,也使统计学进入了更为丰富的发展阶段.此后,许多学者从各个角度研究统计学,不断增加新内容,相继提出并发展了相关和回归理论、t 分布以及抽样理论等,使数理统计学很快成为一门比较系统、比较完善的学科.国际统计学界之所以称凯特勒为“近代统计学之父”,就在于他发现了大量现象的统计规律和开创性地应用了许多统计方法,促使统计学向新的境界发展.由于这一学派主要在英美等国发展起来,故又称之为英美数理统计学派.
历经300 多年的发展,目前,统计学已经成为横跨社会科学和自然科学等多学科的科学.统计学是关于如何测定、收集和分析反映客观现象总体数量的数据,进而给出正确认识的方法论科学.从横向看,各种统计学都具有上述共同点,因而能够形成一个学科“家族”;从纵向看,统计学方法应用于各种实质性科学,同它们相结合,产生了一系列专门领域的统计学.由此可见,现代统计学可以分为两大类:一类是以抽象的数量为研究对象,研究一般的收集数据、整理数据和分析数据方法的理论统计学;另一类是以各个不同领域的具体数量为研究对象的应用统计学.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




