中点公式、MATLAB求解、收敛性和快速性比较

利用插值型公式，两点插值：

三点插值（中点公式）：

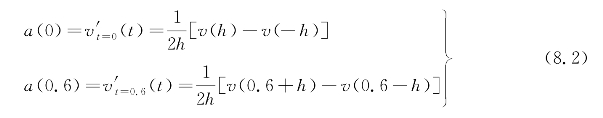
通过不断减小h的值来逼近该点处真实的导数［注意：伴随着h的减小会由于计算v（a＋h）和v（a-h）而产生舍入误差，使逼近效果变差，因而h的值不宜太小］。

同时，类似地，可以像数值积分的外推方法一样，对以上计算出的导数值通过外推的方法加速收敛的速度，记，m＝1，2，…，其中m为外推次数，接着建立类似的表格，如图8.2所示。G0（h）用中点公式来代替：

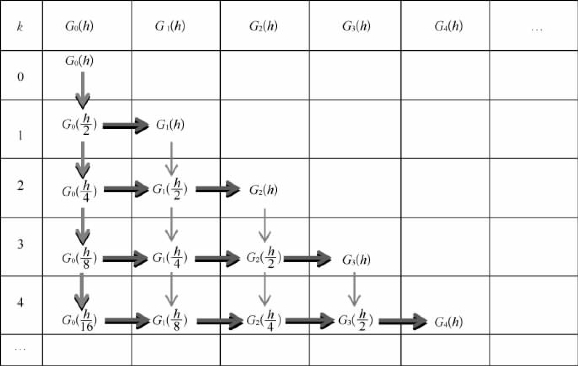
图8.2　递推表格示意

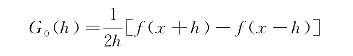
接下来通过MATLAB对上述三种方法进行求解，开始时选取h＝0.1。

MATLAB代码如下：

比较说明方法的收敛性和快速性：

a.两点公式的计算结果为：

t＝0时的加速度为-1.192 768 07，t＝0.6时的加速度为0.901 63。(www.xing528.com)

b.中点公式的计算结果为：

t＝0时的加速度为-1.192 768 07，t＝0.6时的加速度为0.901 63。

c.外推后得到的结果见表8.1、表8.2。

表8.1　t＝0时的加速度

续　表

表8.2　t＝0.6时的加速度

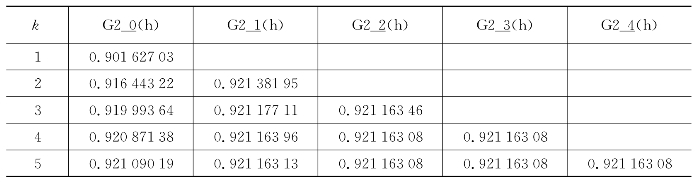
t＝0时，a的真实值为-1.272 082 35；

t＝0.6时，a的真实值为0.921 163 08。

从上述结果可看出，此时两点公式和中点公式的结果恰好一致，但与实际值相比仍有较大误差，

E0＝0.079 314 28，E0.6＝0.019 533 08

而针对外推的方法（以t＝0为例），可以看出，第一次外推的结果-1.271 522 83便已经与连续内推4次的结果-1.271 763 78接近了，而且在G3（h）时便已经与真实值相差无几了。因而从此例可说明外推相比内推大大地加快了收敛速度，每次计算后精度都会有较大提高。