数值分析中的插值点取法及龙贝格外推矩阵

1）牛顿-柯特斯公式法

由于在给出的数据中n＝6，因此可以根据牛顿-柯特斯系数表（表7.11）得出对应系数。

表7.11　牛顿-柯特斯系数

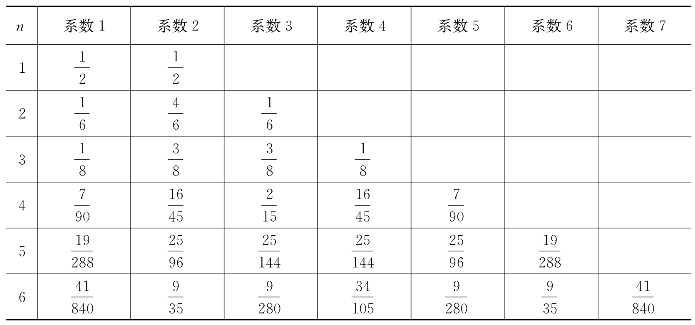
根据题目中所给出运动过程的等效力矩，可以取n＝6所对应的系数，代入表7.10对应的曲柄旋转过程中的等效力矩，可直接得到求积公式如下：

直接计算可得，将该结果代入式（7.30）可得ω＝4.008。

2）龙贝格外推法

由于内燃机运动是一个典型工程问题，无法直接得到Me（φ）的解析表达式，仅仅给出了几个φ与其对应的等效力矩。因此，龙贝格外推方法无法直接应用，需要先通过插值的方式给出近似的原函数，然后对该函数应用此方法。插值点取已知条件中φ所对应的等效力矩值，并根据外推法的需要，将φ＝0、11.25°、22.5°、33.75°、45°、56.25°、67.5°、78.75°、90°九个角度代入得到的插值函数，得出与这些角度对应的近似函数值，作为龙贝格外推法的f（xk）使用。

插值方法可使用拉格朗日插值或牛顿插值，本案例使用拉格朗日插值方法。

龙贝格内推公式为

龙贝格外推公式为

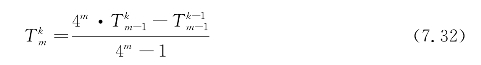
先利用内推公式推出第一列，然后根据外推得到矩阵中其余结果即可。由此得到龙贝格外推矩阵，见表7.12。

表7.12　龙贝格外推矩阵(www.xing528.com)

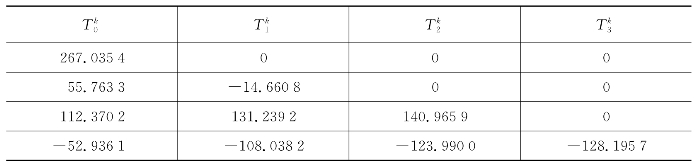
根据龙贝格外推所得，当φ＝90°时，角速度ω＝4.1510 rad/s。

3）稳定性与精度比较

观察龙贝格外推矩阵可以发现，由于没有得到该等效曲柄运动的真实函数，而是用插值的方法去逼近原函数，因此在除了插值节点以外的节点上产生了较大的误差，而这些误差都被带进龙贝格外推公式中，导致外推得到的结果并不收敛，因此无法直接使用龙贝格外推公式。

从精度上分析，牛顿-柯特斯公式在n＝6时有7阶精度，但由于牛顿-柯特斯公式在n＞7时不稳定，因此7阶精度为较高且较准确的数字。龙贝格外推公式虽然无法使用，但根据外推法的性质，在此处n＝8，因此精度高于牛顿-柯斯特公式。

若是在有原函数的情况下使用数值积分，龙贝格外推得到的精度会更高，因此推荐使用龙贝格外推公式；而对于原函数未知的情况，为了力求稳定与收敛，建议使用牛顿-柯特斯公式。

MATLAB代码如下。

龙贝格外推法：

参考文献

［1］张德丰.MATLAB数学实验与建模［M］.北京：清华大学出版社，2014.

［2］郑勋烨.计算方法及MATLAB实现［M］.北京：国防工业出版社，2015.

［3］向华，李大美.数值计算及其工程应用［M］.北京：清华大学出版社，2015.