牛顿-柯特斯公式和龙贝格求积外推公式比较

分析上述问题，设

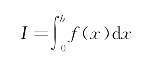
代入式（7.3），则有

针对该问题，首先需要解决在x＝0处的值。

7.4.2.1　计算公式

1）牛顿-柯特斯公式

对于数值积分求积分公式

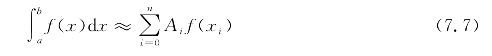
其中

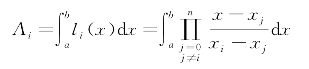
将积分区间［a，b］分成n份，步长，求积节点为xi＝a＋ih（i＝0，1，2，…，n），令x＝a＋th，则拉格朗日插值基函数为

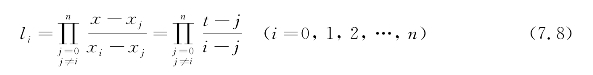
求积系数Ai可表示为

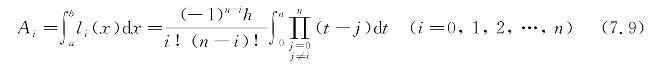
令

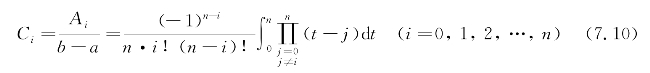
称Ci为柯特斯系数，则求积公式可化为

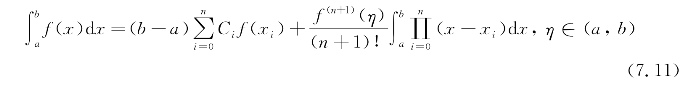
2）龙贝格求积外推公式

对于数值积分求积分公式

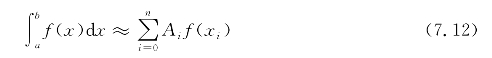
先用梯形公式计算积分近似值

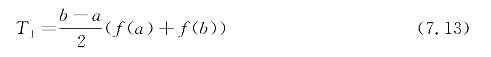
将区间逐次分半，令区间长度

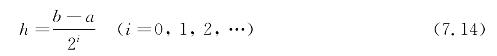
计算

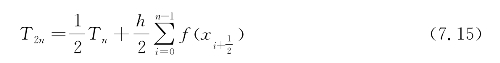
然后用三个加速公式求积分：

梯形加速公式

抛物线加速公式

龙贝格求积分公式(www.xing528.com)

控制精度，直到前后两个积分值R2n和Rn满足：

当｜R2n｜≤1，满足（绝对误差）

当｜R2n｜＞1，满足（相对误差）

则终止计算并取R2n作为积分的近似值，否则，将区间再对分，重复以上步骤，直到满足精度为止。

要求精度

e＝10-5

7.4.2.2　MATLAB代码

1）牛顿-柯特斯公式

2）龙贝格求积外推公式

3）数值积分计算主程序

4）比较说明方法的收敛性和快速性

运行程序得

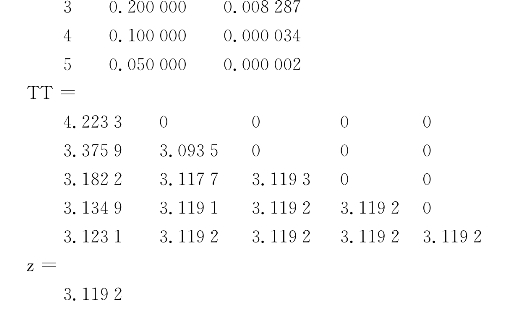
其中，y和z分别为使用牛顿-柯特斯公式和龙贝格求积外推公式数值积分得到的结果，Ck为柯特斯系数，Ak为牛顿-柯特斯公式每项求积系数。表7.6、表7.7为使用龙贝格求积外推公式数值积分的运算过程。将结果制表，有

表7.6　龙贝格求积外推

表7.7　龙贝格求积外推计算步骤

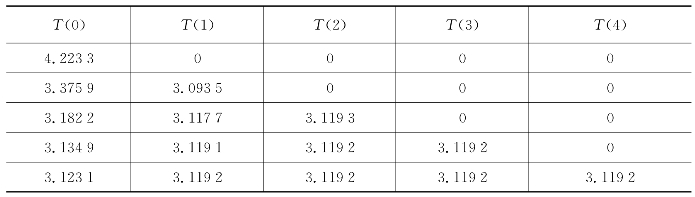
表7.8　数值积分结果

对比可得，两种方法在本例均收敛，得到了相似的结果（表7.8）。考虑到牛顿-柯特斯公式仅计算了四阶积分，无须迭代，而龙贝格求积外推公式也仅迭代了5次，故两方法在本例收敛速度几乎相同。取结果为3.119 2，即

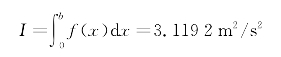
得