牛顿-柯特斯和龙贝格积分算法比较

由动量守恒原理列出等式并整理，可得火箭向上的速度由以下公式计算：

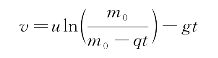
（1）牛顿-柯特斯（复合辛普森）公式求积分：将区间等分为n＝6份（n为偶数）并计算积分；观察n＝4，6，8，10，12时的积分变化。

（2）龙贝格外推公式求积分：设置精度为eps＝1e-10；将两种积分结果进行比较。

1）牛顿-柯特斯（复合辛普森）公式求积分

%复合辛普森积分

2）龙贝格外推公式求积分

由程序运算结果可知：

N＝6的复合辛普森积分：1.087 988 093 684 766e＋04；(www.xing528.com)

精度为1e-10的龙贝格积分：1.087 961 940 489 716e＋04。

由接下来的分析可知，龙贝格积分精度更高，牛顿-柯特斯公式进行的（六等分区间）积分精度远远不够，需要再提高等分区间的个数，才能达到与龙贝格外推一样的精度。

对于复合辛普森积分，改变等分区间个数n，得到的积分结果见表7.4。

表7.4　改变复合辛普森等分区间个数的积分结果

可以看出在等分区间数较少时，每增加等分区间数精度都会有较大的改变。在本题中精度取n＝20以上为宜。

龙贝格积分，改变精度eps，得到的循环次数见表7.5。

表7.5　改变龙贝格积分精度得到的循环次数

可以看出，龙贝格外推的收敛性较快，能在低循环次数时达到较高的精度，是一种很好的算法［2-3］。