龙贝格求积法与辛普森求积法的应用案例及理论分析

MATLAB程序代码如下：

1）龙贝格求积法

主程序如下：

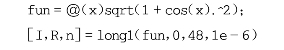
得到计算结果为I＝58.470 469，节点数为n＝2 049。

2）复合梯形求积法

主程序如下：

迭代过程见表7.1。

表7.1　复合梯形求积法的迭代过程

续　表

得到计算结果为T＝58.470 393，迭代步数为11。

3）复合辛普森求积法

(www.xing528.com)

主程序如下：

迭代过程见表7.2。

表7.2　复合辛普森求积法的迭代过程

得到计算结果为S＝58.470 469，迭代步数为11。

4）复合柯特斯求积法

主程序如下：

迭代过程见表7.3。

表7.3　复合柯特斯求积法的迭代过程

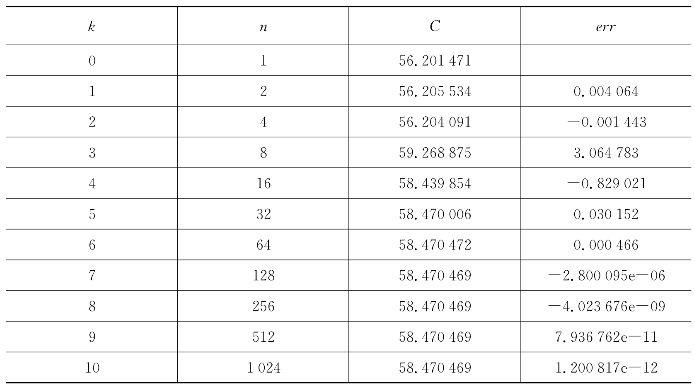
得到计算结果为C＝58.470 469，迭代步数为11。

讨论：用牛顿-柯特斯求积公式时，提高数值积分精度的一个途径是增加求积节点数目。当n增大时牛顿-柯特斯求积公式的数值稳定性变差，也不能提高精度。当f（x）的赋值不太复杂时，复合求积公式可以提高数值积分的精度。根据定义，复合梯形公式的收敛阶是2，复合辛普森公式的收敛阶是4，收敛阶越高，当区间划分加密时，积分近似值就越精确，因此复合辛普森公式的结果更准确，在实际使用中应用更广泛。龙贝格算法是数值稳定的算法，且对任意连续函数，都能保证数值积分收敛到准确值。龙贝格算法程序简单，当f（x）求值不太复杂时，龙贝格算法是常用的实用方法［1］。