【摘要】：选择利用牛顿-柯特斯公式中的三种，即梯形公式、Simpson公式和Cotes公式，对其进行求解。外推方法可以列出如图7.3所示。图7.3外推方法示意MATLAB代码如下：图7.4即为计算结果，可以得出图7.4计算结果首先，比较计算结果和实际结果之间的误差，高斯积分，利用MATLAB算出其值近似为1.772 453 850 9，因而绝对误差为4.021 09×10-5，相对误差为2.268 657×10-5。
选择利用牛顿-柯特斯公式中的三种，即梯形公式、Simpson公式和Cotes公式，对其进行求解。
（1）梯形公式：
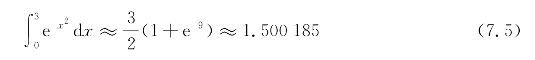
（2）Simpson公式：
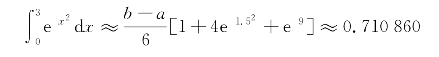
（3）Cotes公式：
实际上，Simpson和Cotes公式即为梯形公式两次内推得到的。为了使结果更精确，采用龙贝格外推公式进行求解：
中m为外推次数，k为内推次数。
内推：
。
注意：这里内推公式只适用于没有进行过外推的项，即下标只为0，；对于外推过的项，再进行内推时，后面须补充一项
；计算本题时对于外推后的项，不再用内推方法进行计算，将内推方法只用于未经外推后项的解。
外推：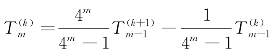
。
外推方法可以列出如图7.3所示（浅色的内推过程本案例不考虑）。(www.xing528.com)
图7.3 外推方法示意
MATLAB代码如下：
图7.4即为计算结果，可以得出
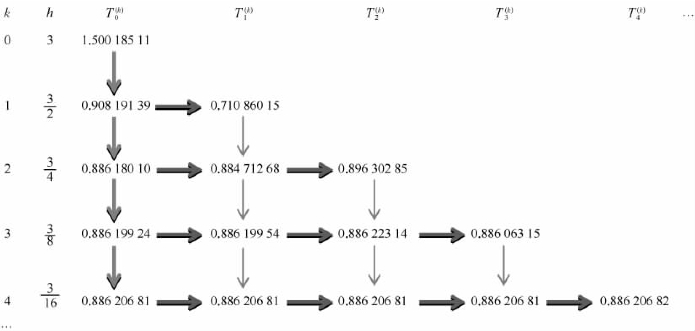
图7.4 计算结果
首先，比较计算结果和实际结果之间的误差，高斯积分
，利用MATLAB算出其值近似为1.772 453 850 9，因而绝对误差为4.021 09×10-5，相对误差为2.268 657×10-5。由此可见，该近似计算精度足够高。
其次，在该外推方法收敛的前提下，发现在此种做法中内推4次便已得到较为精确的值，但是利用外推也需要进行4次才得到较为精确的答案，因而可以发现，外推方法不一定在所有情况下都能增加求积的速度。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
