数值分析典型应用案例：二分法、牛顿法和弦截法计算结果

注意到f（θ）是关于sinθ和cosθ的多项式，所以对于任何给定的根θ，还有其他的根θ＋2π。由于这个原因，把角度θ限制在区间［-π，π］。可以看到f（θ）在这个区间上至多有6个根。

注：求解Stewart平台的前向动力学系统，有x1＝5，（x2，y2）＝（0，6），L1＝L3＝3，，γ＝π/4，p1＝p2＝5，p3＝3。

首先画出f（θ）在［π，-π］上的图像，确定实根个数以及大致位置。

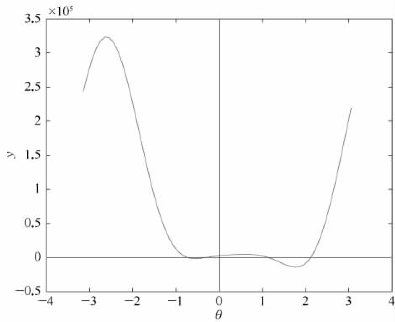
图6.12　y＝f（θ）＆y＝0

由图6.12可知，y＝f（θ）有四个实根，分别在区间（-0.75，-0.65），（-0.35，-0.3），（1.0，1.5），（2.0，2.5）之间。

下面分别采用二分法、牛顿法和弦截法进行计算。

MATLAB代码如下：

首先定义函数f（θ）和其导数f′（θ）。

1）二分法MATLAB的m文件

%二分法求区间（-0.75，-0.65）上的根。

同理，a，b取（-0.3，-0.2），可以求得对应区间上的根。

2）牛顿法MATLAB的m文件

%牛顿法。

同理，x0分别取0.3，1.1，2.0，可以求得对应区间上的根。

3）弦截法MATLAB的m文件

%弦截法求Stewartfun的根。

同理，x0，x1分别取（-0.4，-0.35），（1，1.2），（2，2.2），可以求得对应区间上的根。

程序输出结果：二分法停止迭代的条件为区间长度小于0.000 01，牛顿法和弦截法停止迭代的条件为两次迭代的差值小于0.000 01。

详细计算结果见表6.14～表6.25。

表6.14　二分法在区间（-0.75，-0.65）内的解

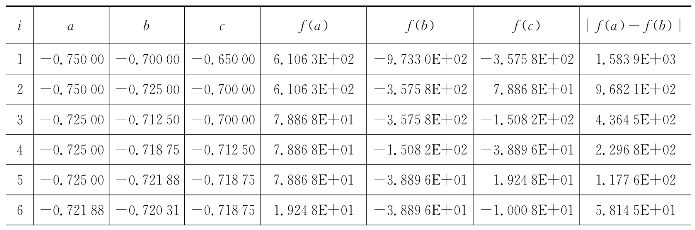
续　表

精度达到要求，最终结果：-0.720 847。

表6.15　二分法在区间（-0.35，-0.3）内的解

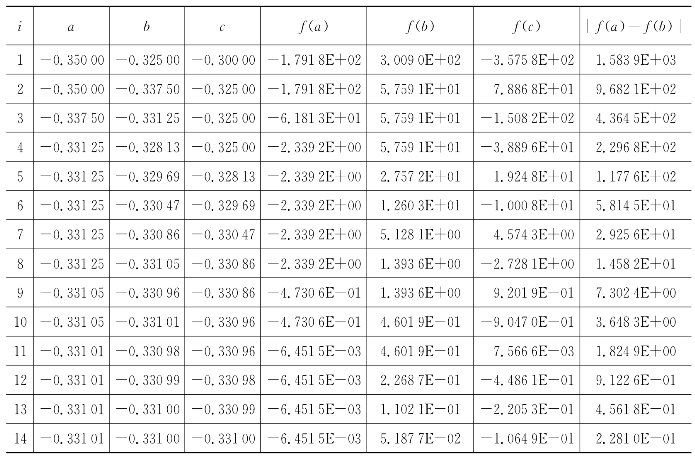
精度达到要求，最终结果：-0.331 003。

表6.16　二分法在区间（1，1.5）内的解

续　表(www.xing528.com)

精度达到要求，最终结果：1.143 688。

表6.17　二分法在区间（2，12.2）内的解

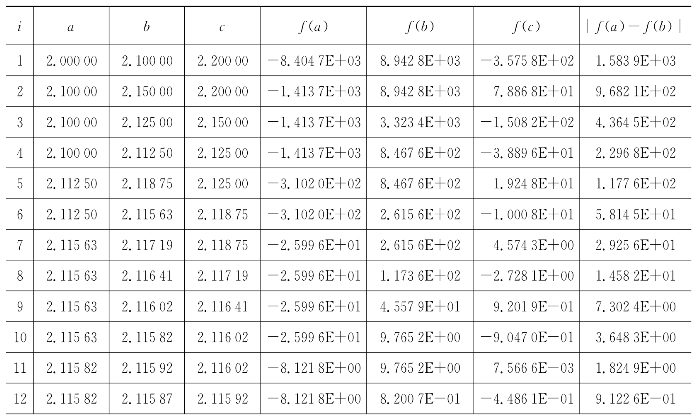
续　表

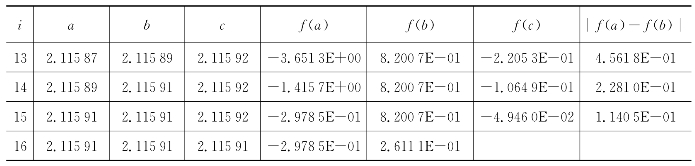
精度达到要求，最终结果：2.115 909。

表6.18　牛顿法在-0.75附近，精度为0.000 01的解

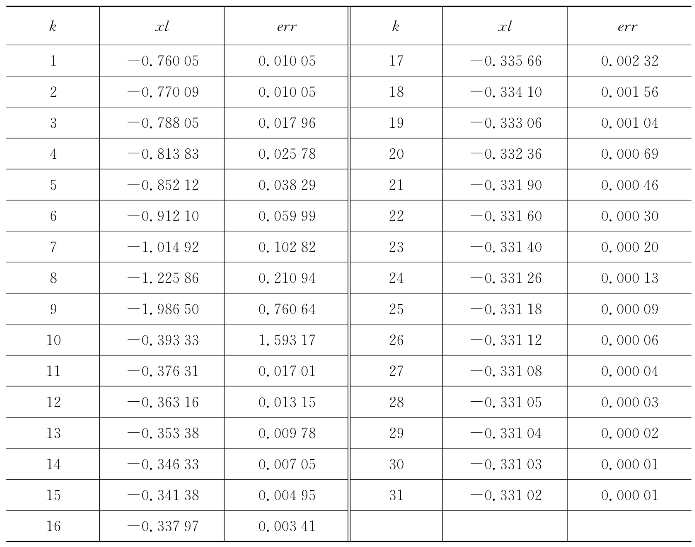
表6.19　牛顿法在-0.3附近，精度为0.000 01的解

续　表

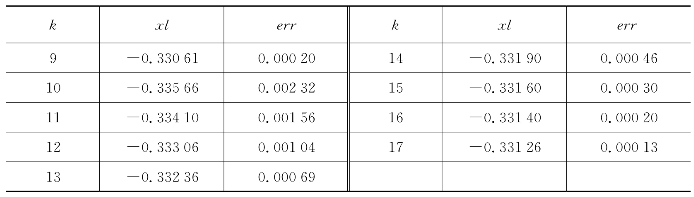
表6.20　牛顿法在1.1附近，精度为0.000 01的解

表6.21　牛顿法在2.0附近，精度为0.000 01的解

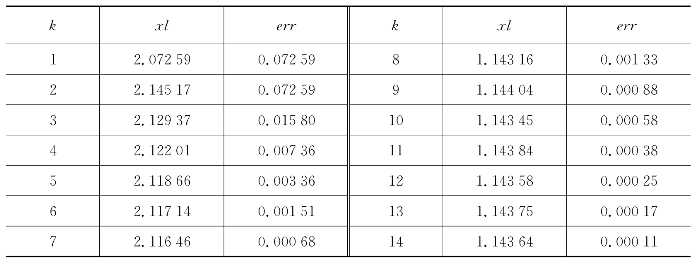
表6.22　弦截法在区间（-0.35，-0.3）内的解

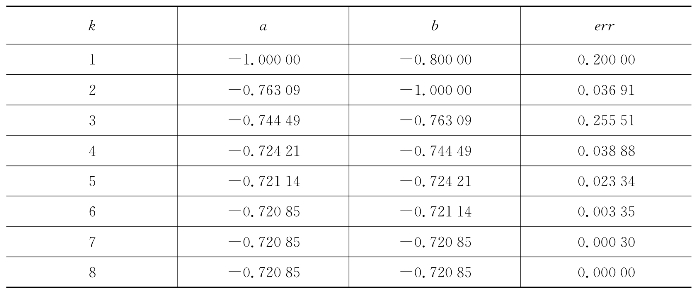
表6.23　弦截法在区间（-0.4，-0.35）内的解

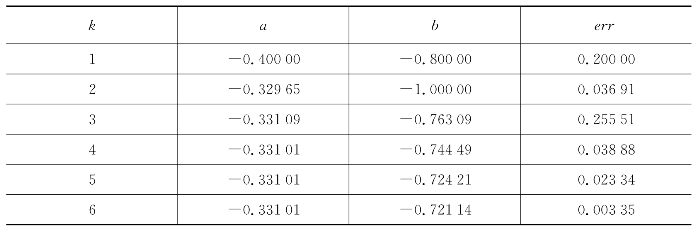
表6.24　弦截法在区间（1，1.2）内的解

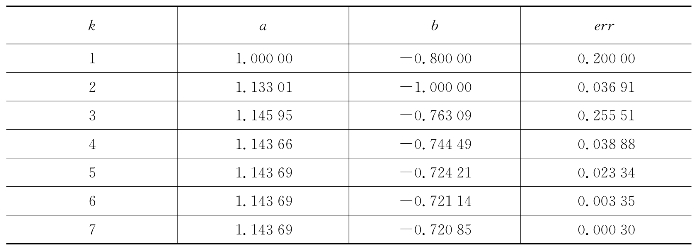
表6.25　弦截法在区间（2，2.2）内的解

续　表

将计算结果整理至表6.26中。在单根区间内二分法总能够收敛到精确值，并可以预计收敛到目标精度需要的计算次数。二分法对函数要求极低，只要确定单根区间即可，但是对于偶重根无法用二分法求解。

表6.26　计算结果整理分析

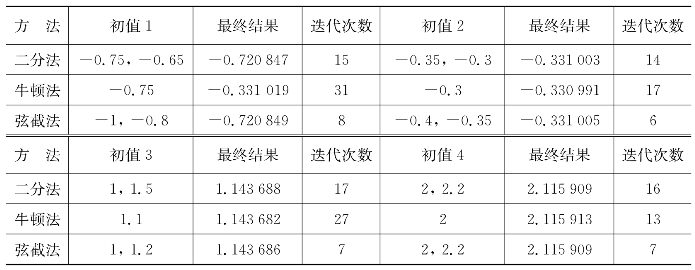
由理论分析，牛顿法的收敛速度是大于二分法的，但在本案例中进行了更多的迭代步数。由于函数比较复杂，牛顿法在收敛过程中会遇到一些问题，如从-0.75为初值进行迭代后最终收敛在0.33附近。从中可以看出，牛顿法是不一定收敛的，收敛与否与初值的选择关系密切。同时，牛顿法的收敛速度和函数有关。

在三种算法应用于本案例中时，弦截法具有最好的收敛性和收敛速度。弦截法避免了对函数的求导，迭代过程相较牛顿法而言也更加保守，具有更好的实用性［2］。

参考文献

［1］原思聪.MATLAB语言及机械工程应用［M］.北京：机械工业出版社，2008.

［2］Timothy Sauer.数值分析［M］.2版.北京：机械工业出版社，2014.