【摘要】：要求精度：ep＝10-5；图6.9y＝f＆y＝0最大迭代次数：it＿max＝100；分别使用二分法、牛顿法和弦截法求方程f＝0在区间［0.2，0.6］上的根。表6.8二分法求表6.9牛顿法求表6.10弦截法求表6.11二分法求表6.12牛顿法求表6.13弦截法求分析以上运行过程并对比，考虑收敛性问题时，二分法一定收敛，牛顿法和弦截法是否收敛还取决于初始点的选取和该点的导数值。
设
问题转化为利用迭代法求非线性方程f（h）＝0的根h*。首先绘制f（h）函数图像以确定根h*的大致区间。
由图6.9可见，方程f（h）＝0在区间［0.2，0.6］上有两根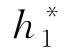
和
，分别位于［0.25，0.3］和［0.45，0.5］上。
要求精度（绝对误差）：ep＝10-5；
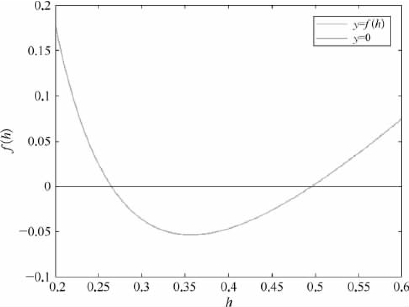
图6.9 y＝f（h）＆y＝0
最大迭代次数：it＿max＝100；
分别使用二分法、牛顿法和弦截法求方程f（h）＝0在区间［0.2，0.6］上的根。
MATLAB程序代码如下：
程序输出结果如下：
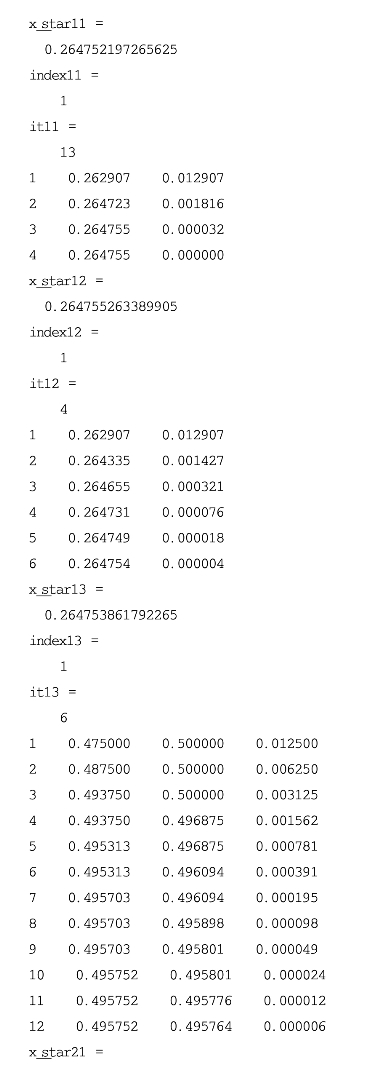
将输出数据整理，运算结果见表6.7。
表6.7 运算结果示例(www.xing528.com)
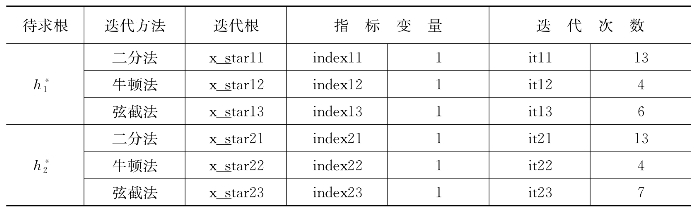
注：index＝1表示递推成功。
将迭代过程制表，见表6.8～表6.13。
表6.8 二分法求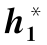
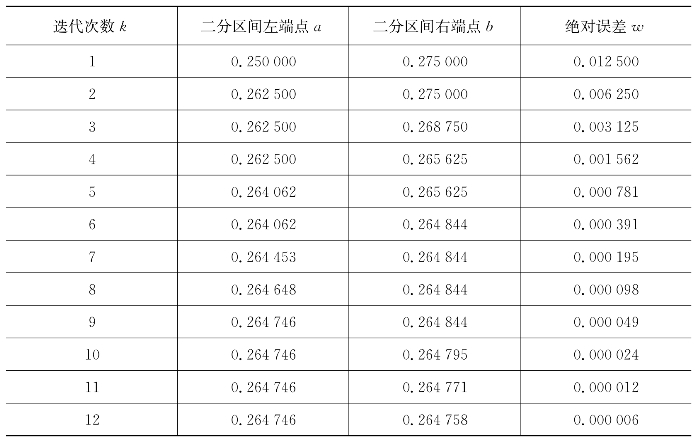
表6.9 牛顿法求
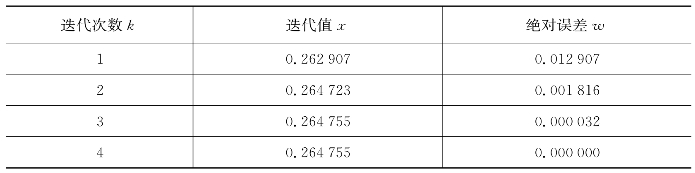
表6.10 弦截法求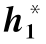
表6.11 二分法求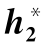
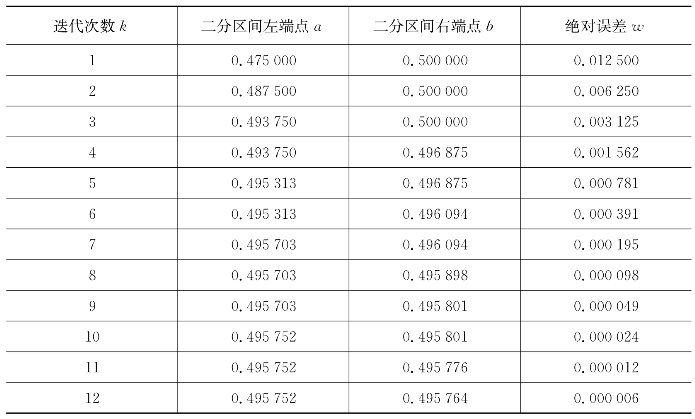
表6.12 牛顿法求
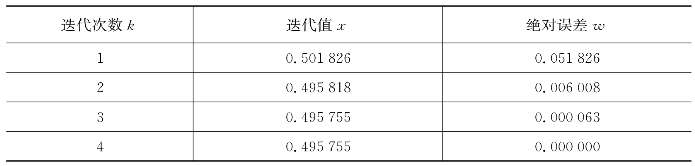
表6.13 弦截法求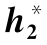
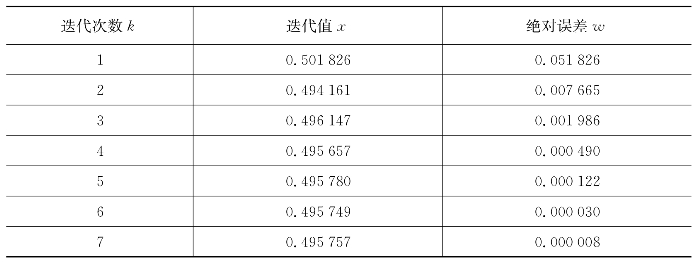
分析以上运行过程并对比，考虑收敛性问题时，二分法一定收敛，牛顿法和弦截法是否收敛还取决于初始点的选取和该点的导数值。在本案例中，二分法、牛顿法和弦截法均收敛，但收敛速度不同：牛顿法收敛最快（迭代4次），而二分法收敛最慢（迭代13次）。通过以上方法，可取
＝0.264 7、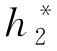
＝0.495 7，以此确定突起上水位的高度。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
