牛顿法、弦截法和简化牛顿法的收敛速度分析

6.2.2.1　三种算法

1）牛顿法迭代方程

对于方程f（x）＝0，有近似根xk，则迭代公式为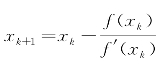。牛顿法的优点是收敛比较快，缺点是每次迭代过程都要计算f（xk）及f′（xk），而且只有初值在真正值附近的时候才能保证收敛。

2）简化牛顿法迭代方程

简化牛顿法可以减少计算量，迭代公式为xk＋1＝xk-Cf（xk），这个方法虽然计算量小，但是只有线性收敛，收敛速度慢。

3）弦截法迭代方程

弦截法在其导数中使用差商代替了导数，其具有超线性的收敛性。弦截法的迭代方程是。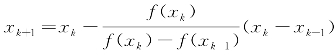

MATLAB代码如下：

6.2.2.2　程序输出结果

1）牛顿法（表6.4）

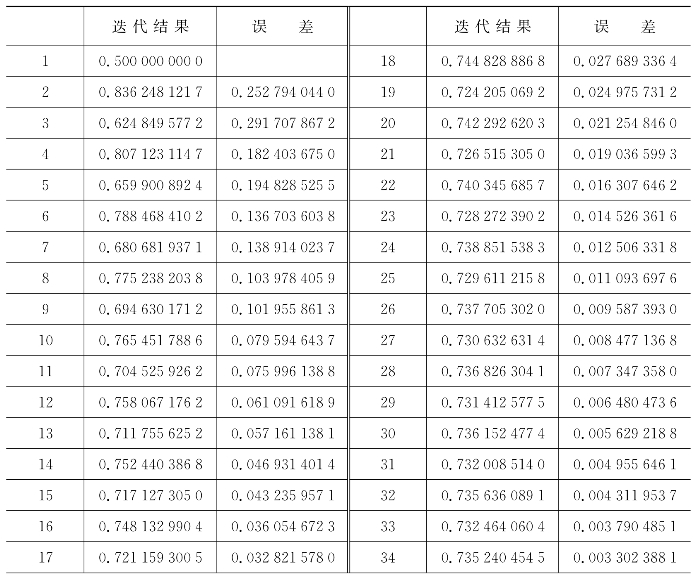
表6.4　牛顿法迭代程序输出结果

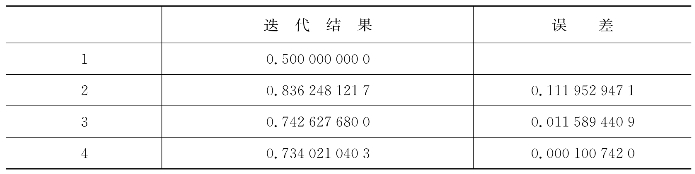
误差变化图像如图6.5所示。

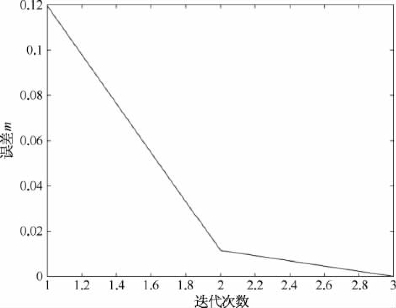
图6.5　牛顿法误差变化图像(www.xing528.com)

2）简化牛顿法（表6.5）

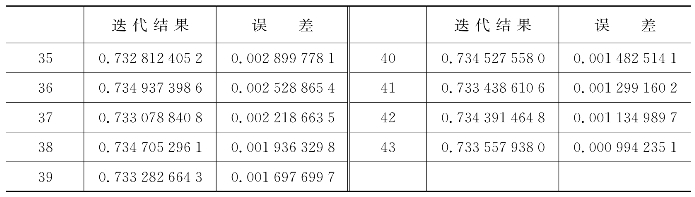
表6.5　简化牛顿法迭代程序输出结果

续　表

误差变化图像如图6.6所示。

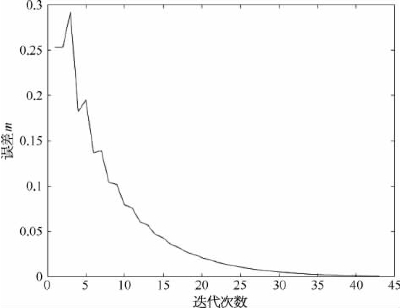
图6.6　简化牛顿法误差变化图像

3）弦截法（表6.6）

表6.6　弦截法迭代程序输出结果

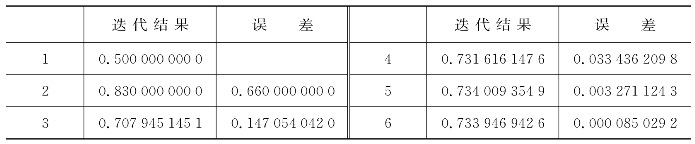
误差变化图像如图6.7所示。

通过图6.5～图6.7可以看出，三种算法都可以收敛，但是牛顿法、弦截法收敛相对较快，简化牛顿法收敛相对较慢。同时牛顿法的计算量非常大。因此综上所述，认为本案例中弦截法是比较好的方法。

最终结果d高度为0.733 557 938 0［1］。

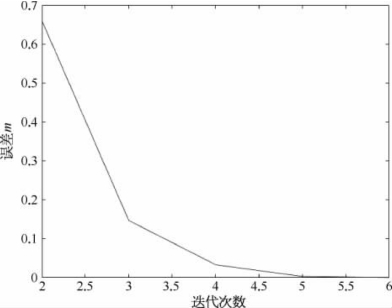
图6.7　弦截法误差变化图像