【摘要】：MATLAB程序代码如下：1）雅克比迭代法雅克比迭代法的源程序m文件如下：迭代过程见表5.2。表5.2雅克比迭代法的迭代过程续表得到计算结果为，迭代步数为32。因此相对而言，高斯-赛德尔迭代法进行了超前迭代，收敛速度增快。列主元-高斯消去法为直接法，可以算得精确结果［1］。
MATLAB程序代码如下：
雅克比迭代法的源程序m文件如下：
迭代过程见表5.2。
表5.2 雅克比迭代法的迭代过程
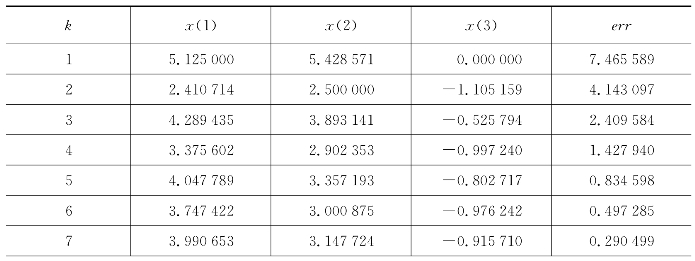
续 表
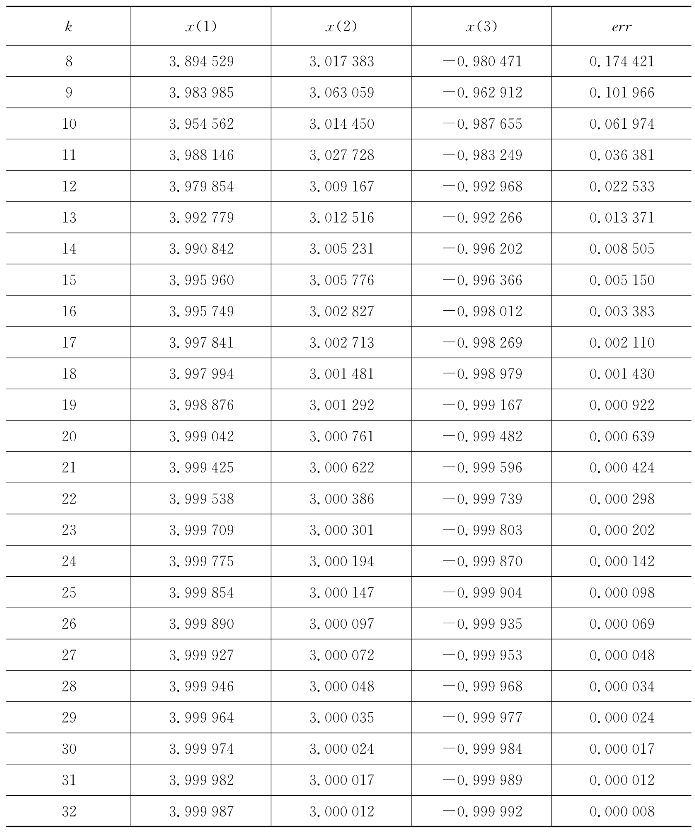
得到计算结果为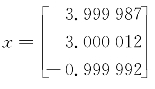
，迭代步数为32。
2）高斯-赛德尔迭代法
高斯-赛德尔迭代法的源程序m文件如下：
迭代过程见表5.3。
表5.3 高斯-赛德尔迭代法的迭代过程(www.xing528.com)
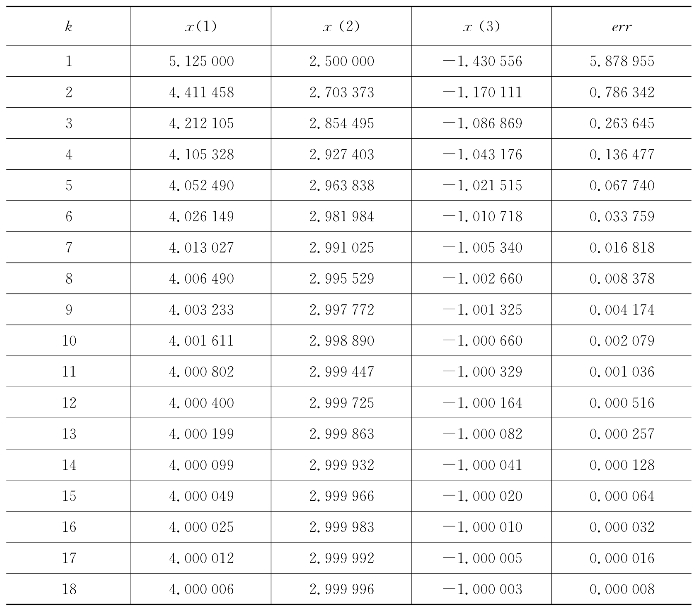
得到计算结果为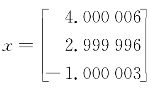
，迭代步数为18。
3）列主元-高斯消去法
列主元-高斯消去法的源程序m文件如下：
列主元-高斯消去法的步骤如下。
Step0：
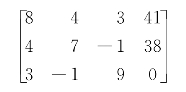
Step1：
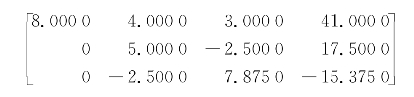
Step2：
得到计算结果为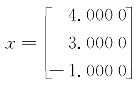
。
讨论：高斯-赛德尔迭代法与雅克比迭代法类似，其区别在于雅克比迭代法每次迭代时只用前面一次的迭代值，而高斯-赛德尔迭代法能充分利用最新的迭代值。即在高斯-赛德尔迭代法中，当进行第（k＋1）次迭代计算解向量x中的元素
时，前面的i-1元素已经算出了第（k＋1）次迭代值（即
，j＝1，2，…，i-1），高斯-赛德尔迭代法要求解析来的n-（i-1）解向量元素直接使用已经算出的
，j＝1，2，…，i-1。因此相对而言，高斯-赛德尔迭代法进行了超前迭代，收敛速度增快。列主元-高斯消去法为直接法，可以算得精确结果［1］。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
