MATLAB画出材料支撑点位置和共振频率散点

首先利用MATLAB画出三种材料支撑点位置和共振频率的散点，如图4.2所示。

图4.2　三种材料支撑点位置和共振频率散点图

＋—玻璃棒；×—黄铜棒；°—钢棒

从点的分布情况可推测曲线形状为抛物线或双曲线，因而针对该数据可以采用二次多项式y＝a1x2＋b1x＋c1和双曲线函数（实轴和y轴平行），同时补充三次多项式函数逼近函数y＝a3x3＋b3x2＋c3x＋d。

在做双曲线逼近时，为了方便计算，将函数变量替换一下，令y（1）＝y2，则y（1）＝a2x2＋b2x＋c2。

可以利用法方程组对上述函数中的未知系数进行求解如下。

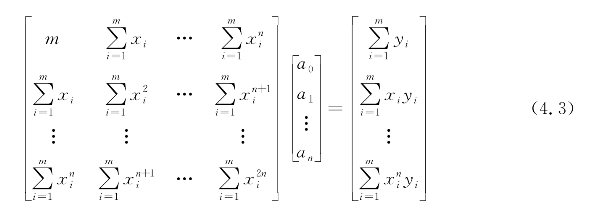
MATLAB代码如下：

程序输出结果如图4.3所示。(www.xing528.com)

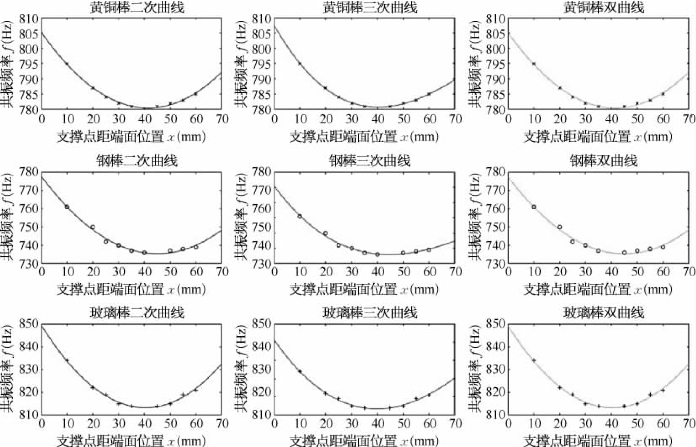
图4.3　针对三种试样棒的拟合

同时获得三种试样棒的拟合函数如下：

1）二次多项式插值函数

2）三次多项式插值函数

3）双曲线插值函数

由此，获得黄铜棒用三种函数拟合得到的共振频率，分别为780.436 Hz、780.682 Hz和780.420 Hz；对比表4.1，黄铜棒用三种函数拟合得到的共振频率误差为0.887 Hz、0.156 Hz和0.935 Hz。可知三次函数拟合曲线的误差最小，从这个角度可看出多项式的阶数越高，拟合越精确。从单调性来分析，这些曲线呈现先减后增的趋势，若超出这个范围，三次多项式以上的函数单调性会发生变化，因而可能与实际值发生较大偏差，因而选择逼近点时要将其选在待求点的附近［1］。