【摘要】：表1.2分形正方体的转动惯量计算结果续表讨论：在数值分析中，我们将在计算过程中误差不会增长的计算公式称为是数值稳定的，否则就是不稳定的。表1.2各计算值中，由于通项公式的计算步数最少，认为该方法得到的计算结果精确性最高，并以此作为参考值。相反地，在递推法2逆推的过程中，每一步的误差都被极大地放大，每次递推都将误差的数量级放大，以至于逆推至I0时得到母体正方体的转动惯量为133［2］。
基于以上分析，求解分形母正方体质量为1、棱长为2的20阶门格海绵的转动惯量。
1）MATLAB算法及释义
m=1；
2）计算结果
计算结果见表1.2。
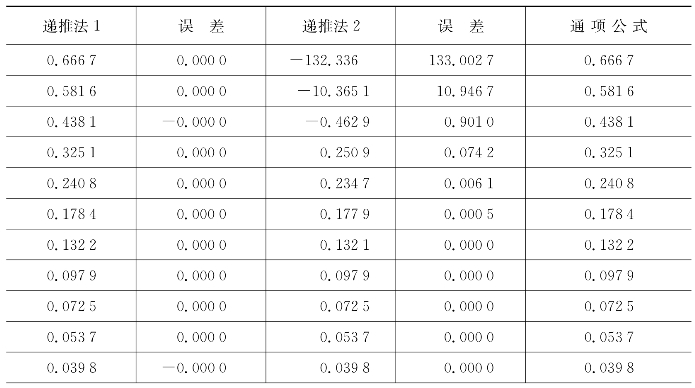
表1.2 分形正方体的转动惯量计算结果
(www.xing528.com)
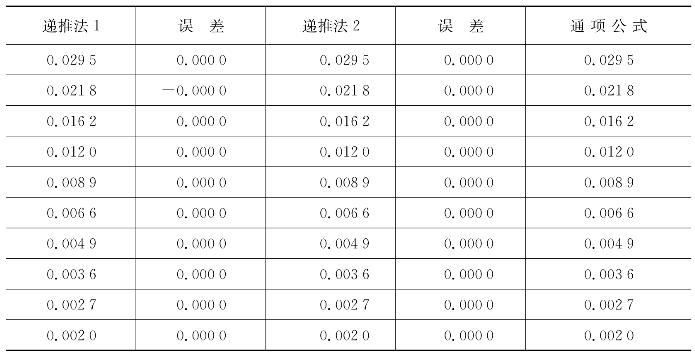
续 表
讨论：在数值分析中，我们将在计算过程中误差不会增长的计算公式称为是数值稳定的，否则就是不稳定的。为了不影响数值分析结果的精确与真实性，在实际应用中，应选用数值稳定的计算公式，尽量避免使用数值不稳定的公式。
表1.2各计算值中，由于通项公式的计算步数最少，认为该方法得到的计算结果精确性最高，并以此作为参考值。可以看到，递推法1得到的结果与通项公式计算值误差极小，事实上，由于递推时的系数
，在每一步递推的过程中，误差在传播过程中被极大地缩小。相反地，在递推法2逆推的过程中，每一步的误差都被极大地放大，每次递推都将误差的数量级放大，以至于逆推至I0时得到母体正方体的转动惯量为133［2］。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
