【摘要】：分形正方体又称门格海绵（Menger Sponge），是数学家卡尔“门格于1926年提出的，它是康托尔集和谢尔宾斯基地毯在三维空间的推广。把正方体每条棱3等分，连接这些等分点，将其分割为27个小正方体，挖去6个面上和中间的1个小正方体，接下来对余下20个小正方体继续同一操作，即得到分形正方体，如图1.8所示。图1.8分形正方体分形立方体的3个惯量主轴是相等的，也即它的3个对称轴。设质量为m、棱长
分形正方体又称门格海绵（Menger Sponge），是数学家卡尔“门格于1926年提出的，它是康托尔集和谢尔宾斯基地毯在三维空间的推广。把正方体每条棱3等分，连接这些等分点，将其分割为27个小正方体，挖去6个面上和中间的1个小正方体，接下来对余下20个小正方体继续同一操作，即得到分形正方体，如图1.8所示。
图1.8 分形正方体
分形立方体的3个惯量主轴是相等的，也即它的3个对称轴。设质量为m、棱长为L的正方体绕其质心轴O的转动惯量I0＝λmL2，取λ＝1/6，那么，第1阶分型正方体的质量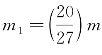
，其转动惯量I1可看作20个线度为母正方体1/3的小正方体绕其惯量主轴的转动惯量的叠加。这20个小正方体中，有8个质心到转轴的垂直距离为L/3，12个质心到转轴的垂直距离为
。
根据平行移轴定理可得
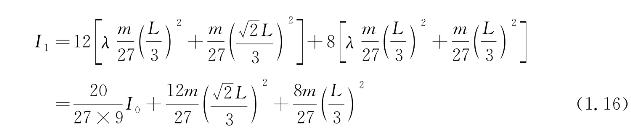
第2阶分型正方体的质量
，它绕质心轴的转动惯量I2可表示为20个长度为1/3倍的第1阶分形正方体绕转轴的转动惯量之和，因此有
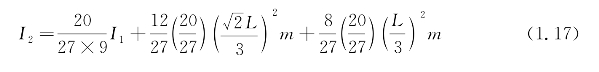
同理，第3阶分形图的质量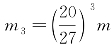
，因而有
以此类推，第n阶分形正方形的质量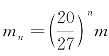
。该分形图形绕其惯性主轴的转动惯量为In，可以看成20个线度为一阶分形正方体1/3倍的分形图形绕惯量主轴的转动惯量的叠加。
根据平行移轴定理可得
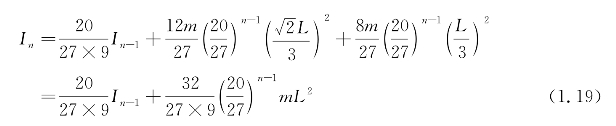(www.xing528.com)
最终由递推公式求数列通项的方法可得
递推算法1
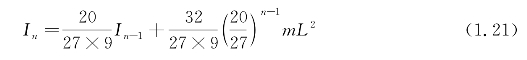
其中
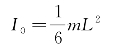
递推算法2
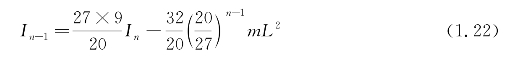
其中
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
