误差不增长的稳定计算公式的应用与原则

1.2.2.1　MATLAB算法及释义

1）阶跃信号

2）三角形信号

3）正弦信号

1.2.2.2　计算结果

图1.5所示阶跃信号，虚线为传统PID，实线为递推PID。(www.xing528.com)

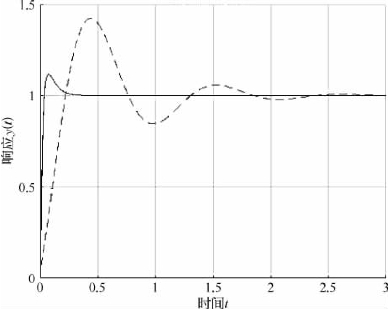
图1.5　阶跃信号

图1.6所示三角形信号，虚线为传统PID，实线为递推PID。

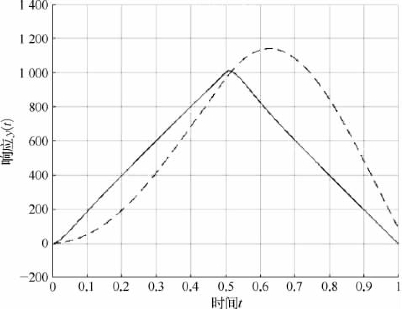
图1.6　三角形信号

图1.7所示正弦信号，虚线为传统PID，实线为递推PID。

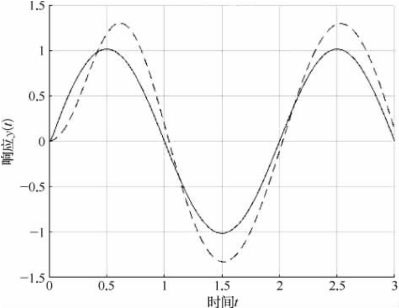
图1.7　正弦信号

讨论：在数值分析中，我们将在计算过程中误差不会增长的计算公式称为是数值稳定的，否则就是不稳定的。为了不影响数值分析结果的精确与真实性，在实际应用中，应选用数值稳定的计算公式，尽量避免使用数值不稳定的计算公式。

对于比较复杂的本案例，递推算法具有很重要的应用意义。递推PID（increment PID control）主要是通过求出增量，将原先积分环节的累积作用进行了替换，避免了误差的叠加，因此在积分环节误差不会增长。算式中不需要累加，不需要对控制过程进行记忆。控制增量Δu（k）的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果，并且Δu（k）表示，计算机每次只输出控制增量，即对应执行机构位置的变化量，故机器发生故障时影响范围小、不会严重影响生产过程。

由上述三种信号相应可以看出，和输入信号相比，在PID参数相同的情况下，虚线（传统PID）波动较大并且滞后。实线（递推PID）是一种比较稳定的算法。