材料力学中的三维应力状态分析问题及解决方法

材料力学中的应力状态分析是强度理论的基础，现有理论支持二维应力状态复杂情形计算分析，但三维应力主值及主轴问题尚未彻底解决。尽管“卡当”公式能确定主值的大小，但计算过程繁杂，且不能给出主轴方位。本案例从二维应力状态转换公式中得到启示，可利用递推法不断旋转参考系方向，使得两个剪应力为0，或一个剪应力为0、另一个近似为0，则可将三维应力转为二维应力状态去进行分析，进而得到三个主应力大小与主轴方向，具体计算方法如下。

图1.1所示为一般三维应力状态单元体，正应力分别为σxx、σyy、σzz，切应力分别为τxy、τyz、τzx。

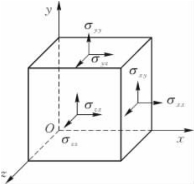
图1.1　三维应力状态单元体

1）第一次旋转

先使σxx＝0，即单元体绕z轴旋转φ角（沿轴正向，逆时针为正），且满足

记新的坐标轴为Ox″、Oy″、Oz″，与其对应的应力值转换为

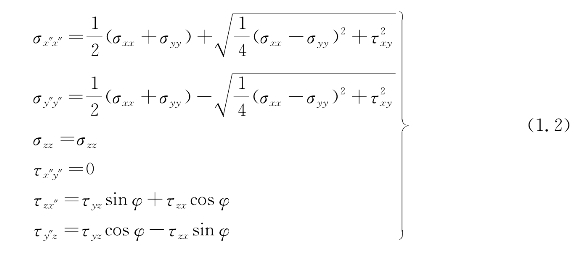
2）第二次旋转

在上述单元体基础上，使单元体再绕x″轴旋转ψ角，且满足

旋转后坐标轴为Ox″、Oy‴、Oz′，且满足τz′y‴＝0，对应的应力为(www.xing528.com)

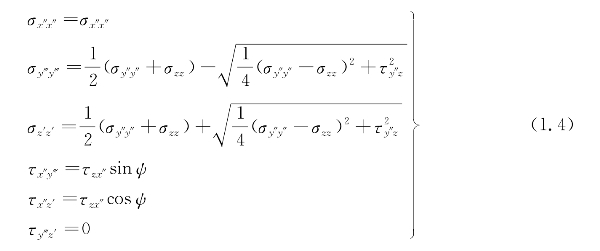
3）第三次旋转

再令上述单元体绕z′轴旋转θ角，且满足

旋转后坐标轴为Ox′、Oy′、Oz′，且满足τx′y′＝0，对应的应力为

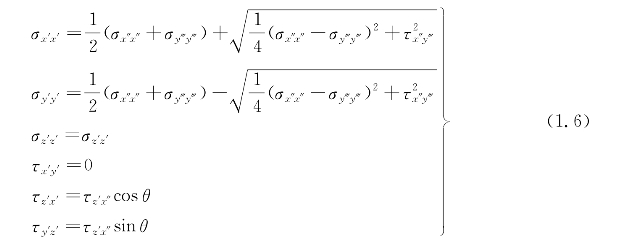
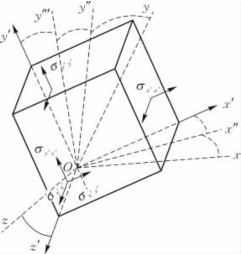
图1.2　三维应力状态单元体的尤拉公式变换

以上即为一个递推过程，得到了新的三个正应力值和三个切应力值。

若记，上述整个递推过程为Ai＋1＝f（Ai）；同时在每次递推内，后一次旋转的角度也均借助了前一次旋转得到的应力值，也利用了递推方法。除了i＝1外，其他的τixy值均为0，那么当另外两个切应力中任何一个接近于0时，即满足一定的精度条件后，便可得出较为精确的三个主应力的值。

主轴方向的确定可通过尤拉公式变换得到每一步旋转后的坐标系各轴相对于原始坐标系的方向，本例对最后的主轴方向不做考虑。每一次的变换结果如图1.2所示。以上每一次递推过程，一共旋转了三次坐标系，每一次旋转都借用了上面的应力值，同时旋转变换带来的应力变换规律相同，所以也可以表示为一次递推关系，即