C语言程序设计-数据排序示例

排序是计算机中最常做的操作之一,是许多应用的基础。掌握一些最基本的排序方法不仅可以方便我们编程,也可以为以后学习其他的编程方法打下基础。排序的基本思想是将一个数据序列分成有序和无序的两个子序列并将有序序列逐步扩大过程。持续这一过程,直至无序序列长度为0,有序序列中包含了所有待排序数据为止。如图6-3所示。

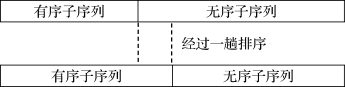
图6-3　数据排序过程示意

排序过程中,依据所采用的扩大有序序列方法的不同,可以分为冒泡排序、选择排序和插入排序等。这里列出了几种不同的排序方法,不一定要大家都全部掌握,但是最少应该能够熟练使用其中的某一种方法对数据进行排序。下面分别介绍。

1.冒泡排序

冒泡排序的基本思想是将相邻的数据两两比较,如前边的值大于后边的值,则将二者交换位置。在此过程中“大数下沉,小数上升”,就像水中的气泡一样,故此叫作冒泡排序。加入有18、53、24、3、16等5个数据参与排序,其排序过程如图6-4所示。

图6-4　前两趟冒泡排序示意

从图6-4可以看出,在进行冒泡排序时,每一趟都是从数据的最前边(0单元)开始,依次拿相邻的两个进行比较,如果前边的数据大于后边的数据,则交换两个数据的位置。这样经过第一趟的比较以后,在数组的最后得到最大值53。第二趟仍然从0单元开始两两比较、交换,最后在数组的倒数第2个单元得到最大值24。以此类推,直到整个数组有序为止。由此可见,冒泡排序的有序子序列是产生在数组的后半部分,初始时有序子序列长度为0,并随着一趟趟的冒泡而逐渐变长。

假设有n个数据参与排序,实现冒泡排序时应考虑如下问题:

(1)排序时总共要进行多少趟冒泡?由于冒泡排序中一趟冒泡只能产生一个最大值,因此n个数据参与排序时总共要进行n－1趟冒泡,剩余的0号单元一定是所有数据中最小的。

(2)每一趟冒泡过程中要进行多少次比较?第一趟冒泡排序中有n个数据进行两两之间的比较,因此总共比较n－1次。在第一趟冒泡结束后,在数组的第n－1号单元得到一个最大值,因此在第二趟冒泡过程中,n－1号单元不用再参与比较(已经是最大的),因此总共有n－1个数据两两比较,总共进行n－2次的比较。以此类推,第i趟排序过程中,总共要进行n－i的比较。

一趟冒泡只能产生一个最大值,因此冒泡排序是一个双重循环。程序实现中可用外循环控制冒泡趟数,用内循环控制每一趟冒泡中的相邻单元间的比较。

【例6-7】输入n(n＜20)和n个整数,并用冒泡排序方法对这n个整型从小到大排序,输出排序结果。

根据前边分析,实现源代码如下:

请大家结合源程序深入领会冒泡排序的思想。

2.插入排序

利用例6-5中“在有序序列中插入一个值并仍保持数据有序”的思想也可以完成数据的排序,这就是插入排序。假设有n个数据参与排序,排序过程如下:

(1)将数据序列分为两个部分,0单元为有序子序列,1～n－1单元为无序子序列。

(2)将1单元的值插入前边有序子序列中并保持0～1单元有序,此时2～n－1单元为无序子序列。

(3)将2单元的值插入前边有序子序列中并保持0～2单元有序,此时3～n－1单元为无序子序列。

以此类推,直至将n－1单元的值插入有序子序列,排序过程完成。

由此可见,插入排序中有序子序列在数组的前边,无序子序列在数组的后边,初始时将0单元单独看作长度为1的有序子序列,随着不断地插入,有序子序列逐渐扩大,直至全部数据有序为止。(www.xing528.com)

结合以上分析,插入排序源代码如下:

程序运行结果如下:

请输入待排序数据的个数,待排序数据不超过20个:10

请输入10个待排序的数据:100　20　3　7　80　56　34　87　45　92

插入排序结果:3　7　20　34　45　56　80　87　92　100

插入排序中总共需将1～n－1单元中的每一个值往前边有序子序列中插入,因此总共要循环n－1回。程序中在完成a[i]的插入时,首先将a[i]的值暂存到变量t中,因为在比较并后移数据的过程a[i]单元的值可能会被覆盖;外循环中循环变量i不仅控制外循环次数为n－1次,同时表示要插入的是a[i]单元的值;由于0～i－1单元为有序序列,因此内循环中的循环变量j从i－1开始,由后往前依次和t值进行比较并将大于t的值后移一个单元,从而给t中的值腾出插入位置。

这就是插入排序,请结合源程序深入体会插入排序的思想,并把握“插入”这一核心概念在该方法中的应用。

3.选择排序

使用例6-6中选择最小值和最小值下标的思想,也可以完成数据的排序,这就是选择排序。假设数组a中存放了n个整数,欲对这n个整数进行选择排序,其过程如下:

(1)从0～n－1单元中选出一个最小值,并将之放入a[0]单元;

(2)从1～n－1单元中选出一个最小值,并将之放入a[1]单元;

以此类推,直至从a[n－2]和a[n－1]单元中选出一个最小值并将之存入a[n－2]单元,此时a[n－1]单元中就是一个最大值,所有数据有序。第i趟选择如图6-5所示。

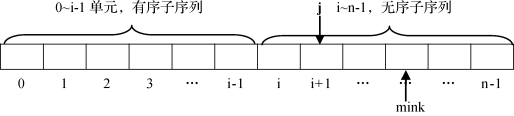
图6-5　第i趟选择示意

由图6-5可知,第i趟选择最小值时其选择范围是i～n－1,并将在本轮选择结束后得到的最小值放入a[i]单元。但是要注意的是,在排序过程中我们并不会关心最小值的“值”具体是多少,只要知道它是当前选出的最小值即可,因此排序过程中将只记录最小值的下标mink,并在本轮选择结束后将之与a[i]单元交换位置即可。这里的mink就是“擂台”,第一个上擂台的就是“i”,j从i＋1开始依次取每一个单元参与比较,源代码如下:

程序运行结果如下:

请输入待排序数据的个数,待排序数据不超过20个:10

请输入10个待排序的数据:100　20　3　7　80　56　34　87　45　92

选择排序结果:3　7　20　34　45　56　80　87　92　100

以上共介绍了三种排序方法,要求必须至少掌握一种并能够熟练进行数据的排序操作。其他两种可以作为了解,一方面开阔思路,另一方面可以使我们更加熟悉一维数组的操作。