郭书春数学史自选集（下册）-步度准确，公私共利

自春秋时期私田出现，度量土地面积就是人们生产生活的首要问题。《九章筭术》、秦简《数》、汉简《筭数书》有正方形、长方形、梯形、圆、弓形、环形、球冠形等各种形状的面积公式。随着社会经济的发展，人口的增加，人们不断开荒，出现各种复杂形状的田地。南宋时期人们整治沿海、沿湖新涨的沙田、湖田，并人造圩田。这些田地的形状更不规则，很多人计算面积的方法是错误的。土地面积计算不准确，如果多了，就要多交租税，对田主不利，如果少了，国家的收入会受损失。秦九韶的《数书九章·序》田域类系辞说：

魁隗粒民，甄度四海。苍姬井之，仁政攸在。代远庶蕃，垦菑日广。步度庀赋，版图是掌。方圆异状，衺窳殊形。叀术精微，孰究厥真。差之毫厘，谬乃千百。公私共弊，盍谨其籍。[13]

秦九韶在这里充分阐发了准确计算田地面积对国计民生的重大意义。秦九韶在《数书九章》田域类中对许多复杂形状的田地都提出了正确的计算方法，有的运用当时最先进的正负开方术和三斜求积公式求解。比如《数术九章》田域类的“漂田推积”题是（略去答案）：

问：三斜田被水冲去一隅而成四不等直田之状。元中斜一十六步，如多长；水直五步，如少阔；残小斜一十三步，如弦；残大斜二十步，如元中斜之弦；横量径一十二步，如残田之广，又如元中斜之句，亦是水直之股。欲求元积、残积、水积、元大斜、元中斜、二水斜各几何。

术曰：以少广求之，连枝入之，又句股入之。置水直，减中斜，余为法。以中斜乘大残为大斜实。以法除实，得元大斜。以残大斜减之，余为水大斜。以法乘径，又自之，为小斜隅；以水直幂并径幂，为弦幂。又乘径幂，又乘中斜幂，为小斜实。与隅可约约之。开连枝平方，得元小斜。以残小斜减之，余为水小斜。以水直幂并水大斜幂，减水小斜幂，余半之，自乘于上；以水直幂乘水大斜幂，减上；余，四约之，为水实；一为从隅，开连枝平方，^[3]得水积。以水直并中斜，乘径，为实；以二为法；除之，得残积。以残积并水积，共为元积。有分者通之，重有者重通之。[13]

图1

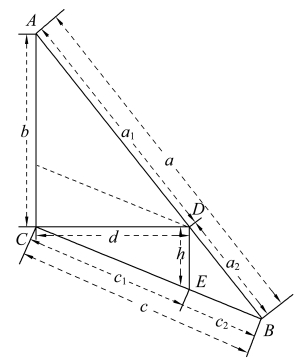
图2

见图1，设三斜田为ABC，记其面积为S，BC为大斜，记为a，AC为中斜，记为b，AB为小斜，记为c。冲去的三角形为EBD，其面积称为水积，记作S2。因为ACDE是四不等直田，故DE∥AC，其面积称为残积，记作S1。记残大斜CD为a1，残小斜AE为c1，水直DE为h，残大斜CD为a1，径AD为d。（见图2）术文的第一段是求原来的大斜BC：过D作DF∥AE，则三角形FDC～三角形ACB，因此，故元大斜BC即a=。(www.xing528.com)

术文的第二段是求被冲毁的三角形EBD的大斜即水大斜BD：

a2=a-a1=-a1。

术文的第三段是求原来的小斜AB：由三角形FDC～三角形ACB，得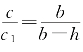，（b-h）c=c1b。而由勾股形ADE，得c21=h2+d2，故[（b-h）c]2=c21b2，于是[（bh）c]2=（h2+d2）b2，或（b-h）2c2=（h2+d2）b2，此即以小斜c为未知数，以（b-h）2为二次项系数，以（h2+d2）b2为被开方数的二次方程。开方即得小斜。由于没有一次项系数，秦九韶称之为“开连枝平方”。不知为什么秦九韶又以d2乘各项。

术文的第四段是求被冲毁的三角形EBD的小斜BE：水小斜c2=c-c1。

术文的第五段是求被冲毁的三角形EBD的面积即水积S2：以水积S2为未知数，以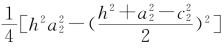为被开方数，即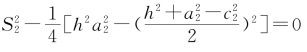的解就是水积。这里用到了卷五三斜求积问的公式，它与海伦公式等价^[4]。

术文的第六段是求被冲毁后剩余的四不等直田ACDE的面积，称为残积S1：这是一个梯形，应用其面积公式，得S1=（h+b）d。

术文的第七段是求原来三角形ABC的面积S：S=S1+S2。

圆满地解决了复杂形状的田地面积计算问题。