数学著作的读者与作者的和谐关系

中国古代数学家在撰写数学著作时一般要预设读者是按照作者的思路，与他站在同一个角度考虑问题的。起码有以下几个方面反映出这个特征。

首先，中国古代数学著作中有许多数学概念，有些概念，在先秦墨家的《墨经》中载有其定义，比如“圜，一中同长也”[6]，就是一个堪与欧几里得的《几何原本》中圆的定义媲美的定义。但是在《九章筭术》、秦简《数》、汉简《筭数书》等数学著作中的数学概念，不管是方田、广、从、高、袤、邪、圆田、箕田、邪田、弧田、宛田、环田、方堢壔、圆堢壔、城、垣、堤、沟、堑、渠、堑堵、阳马、鳖腝、方锥、圆锥、方亭、圆亭、刍甍、刍童、盘池、曲池、冥谷、羡除、勾、股、弦、勾股形等现今归之于几何的大量概念，还是并、合分、差、减、减分、课分、乘、乘分、除、经分、约、率、衰分、少广、同、程、方程、直除、正、负等运算概念，其涵义，作者当然是明确的，但是都没有明确界定，而需要读者根据问题的假设、术文甚至答案，也就是按照作者的意图来确定它们的意义，久而久之，形成约定俗成的共识。直到三国魏刘徽才对某些概念作出明确的定义。

其次，对数学运算、推理中所使用的许多原则、原理，数学著作中并没有列出或表述，而是心照不宣地使用，比如解决图形的面积、体积与解勾股形等问题中所运用的出入相补原理必须借助于两个前提：一个图形平移或旋转不改变其面积或体积，一个图形被分割成若干部分，所有这些部分的面积或体积之和等于原面积或体积，这两条都作为不言自明的公理来使用。甚至对某些明确表述的原理，有的也是当作已知的公认的知识。比如，刘徽在解释方程术的直除法是正确的时候说：“举率以相减，不害余数之课也。”是说方程的一行与另一行整行相减（加），不影响方程的解。这个命题符合现代线性代数理论，但是是需要证明的，而刘徽却直接拿来应用。又如，关于截面积原理，刘徽说：“上连无成不方，故方锥与阳马同实。”方，训层，这是说，如果同底等高的方锥与阳马的每一层都是相等的正方形，则它们的体积相等。《九章筭术》少广章开立圆术李淳风等注释引祖暅之说：“夫叠棊成立积，缘幂势既同，则积不容异。”它比刘徽的命题更宽泛：同底等高的两组立体，如果它们等高处的面积（之和）相等，则它们的体积不能不相等。这就是著名的祖暅之原理。这个原理是作为公认的真理被应用的。

第三，数学著作中有一些命题或题目的设问，其条件有时并不完备，读者必须按照作者的未明言的思路去理解，补充某些必要的条件，才能得出正确的结论或答案。上面谈到的祖暅之原理，其“同底等高”也是蕴含在命题中，读者必须按照作者的思路作这样的而不能作其他的理解。又如《九章筭术》粟米章其率术的例题的形式是：

今有出钱A，买物B。欲其贵贱某单位率之，问：各几何？

荅曰：

其u个，个x钱；

其v个，个x+1钱。

按题设，可以列出一个四元不定方程：

ux+vy=A(www.xing528.com)

u+v=B

从各个题目的答案看，是求整数解，并且每单位的价格差1钱，都是题目中没有讲到的。《九章筭术》给出的其率术是：

其率术曰：各置所买石、钧、斤、两以为法，以所率乘钱数为实，实如法而一。不满法者，反以实减法，法贱实贵。

其方法用现代符号写出就是：

其中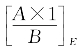是表示的整数部分。

第四，对有些文字的理解，读者应当站在作者的角度择善而从。古代数学著作的有些文字，今人理解起来会有歧义，即使是辩难之风盛行的魏晋，逻辑非常严谨的刘徽，某些话也会有不同的理解。比如在证明刘徽原理时，刘徽用一个黑阳马与一个赤鳖腝拼合成一个堑堵，用三个互相垂直的平面平分该堑堵的长、宽、高，则阳马被分割成1个小黑长方体、2个小黑堑堵、2个小黑阳马，鳖腝被分割成2个小赤堑堵、2个小赤鳖腝。刘徽说：“令赤、黑堑堵各自适当一方。”就字面而言，这里既可以是1个小赤堑堵与1个小黑堑堵拼合成1个小立方体，也可以是2个小赤堑堵、2个小黑堑堵分别拼合成1个小立方体。中国数学史界确实有这二种不同的理解。日本三上义夫提出了这二种可能性，但他倾向于后者[7]。丹麦华道安主张后者[8]，而笔者主张前者[9]。到底哪一种理解对呢？刘徽注的这一段文字虽然是借助于长、宽、高相等的棊讨论，但是后面说“虽方随棊改，而固有常然之势也”，因此，它实际上是讨论长、宽、高不相等的情形。而在长、宽、高不相等时，2个小赤堑堵或2个小黑堑堵是无法拼合成1个小长方体的，只有1个小赤堑堵与1个小黑堑堵才能拼合成1个小长方体。由此可见，只有前者的理解是正确。

中国传统数学中诘难的欠缺，当然造成其理论研究相对于古希腊而言比较薄弱（但不是没有）。但是，坏事在一定条件下可以变成好事。古希腊数学家由于无法解决潜无穷与实无穷的争论，引起了数学危机，并将无穷小和极限思想排除在数学之外。中国古代实际上也存在潜无穷与实无穷的分野，比如名家的“一尺之捶，日取其半，万世不竭”[10]，便是潜无穷小的思想。而墨家的“非半弗则不动，说在端”，“非半，进前取也。前，则中无为半，犹端也。前后取，则端中也。必半，毋与非半，不可也”[6]，则是实无穷小的思想。他们之间也有争论，但是后来的数学家似乎不关心这种争论，也不考虑与1是不是有公度。刘徽径直认为从圆内接正多边形割圆，“割之又割，以至于不可割，则与圆周合体而无所失矣”；而对阳马与鳖腝拼合成的堑堵，每次平分其长、宽、高，无限次的平分之后，会达到“至细曰微，微则无形”的地步；就是说，这都能将无穷小分割进行到底，实现了实无穷小，与墨家、道家的命题一致，而不理会名家“万世不竭”的命题。因此，在刘徽那里，没有发生将无穷小分割排除在数学之外的事情，因而成为世界数学史上第一个将无穷小分割和极限思想用于数学证明的数学家。

而且由于不考虑与1是不是有公度的问题，刘徽在开方不尽时不再“以面命之”，也不像他以前的某些数学家那样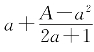，以或以作为根的近似值，其中A是被开方数，a是根的整数部分，而是继续退位求其微数，即以十进分数逼近无理根的近似值。他说：“不以面命之，加定法如前，求其微数。微数无名者以为分子，其一退以十为母，其再退以百为母。退之弥下，其分弥细，则朱幂虽有所弃之数，不足言之也。”刘徽求微数的意义十分重大，它奠定了中国古代圆周率近似值计算领先世界数坛千余年的计算基础。倘无求微数，别说祖冲之精确到8位有效数字，就是像刘徽那样精确到3位或5位有效数字，也是不可能的。