对中国古代数学,人们往往认为成就很大,然而没有理论,与演绎逻辑无关,从未参与过从实践到纯知识领域的飞跃。这些看法一时十分流行,并且因曾被一些现代科学泰斗所引用而成为近年一些论述变量数学未能在中国产生,以至中国近代科学落后的某些文章的论据。事实上,流行的看法即使被科学泰斗所赞同也不能成为讨论的出发点。因为这些看法都是对中国古典数学原著缺乏深入研究的肤受之言,而如果缺乏深入研究,即使一位受人崇敬的现代科学泰斗,他对这一问题的知识未必会超过一位优秀的中国中学生。我们认为,探讨中国古典数学思维方式唯一可行的方法是认真学习并实事求是地分析中国古典数学原著。
一
本文所谓中国古典数学,从时间上界定为先秦至明末。这一段基本上未受外来的尤其西方数学的影响,而元中叶以前是中国数学最辉煌的时期,最能反映中国数学的特点。从先秦到明末的中国数学大体可以分为以下几个阶段:
先秦到两汉以《九章算术》为代表的框架构筑时期。《九章算术》是中国古代最重要的数学经典,它是在先秦九数基础上发展起来的,包括近百个一般公式、解法,其主要部分采取术文统率应用问题的形式,只有很少一部分采取一题一术且术文是具体算式而非一般公式的形式。把《九章算术》说成应用问题集并不符合该书的实际情况,且给人造成其中只是具体解法没有一般公式和程序的误解。
魏晋到唐中叶以刘徽、祖冲之父子为代表的理论奠基时期。刘徽《九章算术注》(263)“析理以辞,解体用图”,对《九章算术》的术文作了全面论证,纠正了其中某些错误,对许多数学概念作了定义,引入了若干新的方法,尤其是无穷小分割和极限思想。他认为通过“事类相推”,数学知识可以整理成一个“约而能周、通而不黩”的体系,像一株“枝条虽分而同本干”“发其一端”的大树[1]。祖冲之父子《缀术》因隋唐“学官莫能究其深奥,是故废而不理”[2],遂失传,目前只知道其少数然而十分重大的成就。
唐中叶至宋元的高潮时期。人们创造乘除捷算法和各种口诀,导致十进小数广泛使用及珠算的产生。贾宪、秦九韶、李冶、杨辉、朱世杰等著书立说,在许多方面取得若干重大成就。
明以后的衰落时期。除珠算术得到普及外,在其他方面几无建树。汉唐宋元数学著作或失传,或莫明其妙。直至明末传教士传入西算,中国数学才有新的起色。
中国古典数学以计算为中心。所有的术文都是计算公式或程序,所有的题目必须运用术文算出答案,几乎没有离开数量关系的关于空间形式及其性质的讨论,这早已为人们所熟知。
中国古典数学的主要形式:一是一般性的公式、解法及其例题即术文统率应用问题的形式,二是应用问题的形式,三是为算经作注。作为中国数学最重要成就的载体,主要取第一、三两种形式,并且大体交叉出现。比如先秦至汉提出了若干一般公式、解法,汉末魏晋南北朝至唐初则为之作注,证明这些方法,建立起理论基础。宋元数学家提出了若干更高深的复杂算法和理论,然而随之而来的明朝数学大衰退,不可能进行论证。这一工作推迟了几百年,是在清乾嘉时期中国古典数学复兴时才完成的。
二
《周髀算经》记载,先秦数学家陈子认为荣方之所以对测高望远之术不能理解,在于他“之于数未能通类”。陈子指出:“夫道术,言约而用博者,智类之明。问一类而以万事达者,谓之知道。今子所学,筭数之术,是用智矣,而尚有所难,是子之智类单。夫道术所以难通者,既学矣,患其不博;既博矣,患其不习;既习矣,患其不能知。故同术相学,同事相关。此列士之遇智、贤不肖之所分。是故能类以合类,此贤者业精习智之质也。”[3]陈子所指出的通类、类以合类是中国古代数学的主要思维方式。
中国古代数学著作很少有如何得出某一术文的思维过程的描述,然而陈子所指出的在大量占有数学问题(博)的基础上,深入研究(习),最后达到知(知类),总结出“言约而用博”的术,无疑是类以合类的一个重要方面,这显然是一归纳过程。比如,人们在大量谷物交换中总结出各种谷物互换的比例关系:粟∶粝∶粺∶糳∶御…=50∶30∶27∶24∶21…,进而总结出粟米互换的今有术:
以所有数乘所求率为实,以所有率为法,实如法而一。[1]
亦即若已知乙的量及甲∶乙=a∶b,则甲=乙÷a×b。
归纳的过程常常要经过多次反复,才能得出正确的认识。圆柱与方柱、圆台与方台、圆锥与方锥在《九章算术》中都是成对出现,当时大约通过两者的大圆与大方(在上述情况下是底),得出其体积之比,由后者推得前者的体积。同样认为球与外切圆柱之比是π∶4,得出错误的公式。可见这种认识未抓住问题的本质。3世纪刘徽则认识到,用以比较的两立体任意等高处的截面积成定比,其体积才成定比。他用两圆柱体正交,其公共部分称为牟合方盖,提出球与外切方盖体积之比为π∶4,指出了解决球体积的正确方向。5世纪祖暅之进而认识到,一组立体与等高的某立体相比较,若任意等高处该组立体截面积之和等于某立体的截面积,则其体积相等,从而提出了完备的祖暅之原理:
夫叠棊成立积,缘幂势既同,则积不容异。[1]
他利用这一原理证明了割出牟合方盖之后的外三棊的截面积等于一倒置阳马同高处的截面积,彻底解决了球体积问题。祖暅之原理经历了几百年的归纳过程才臻于完善。
宋元时代,归纳所得的结果更复杂一些。比如贾宪由开平方、开立方法归纳出开方作法本源即贾宪三角,及造该三角的增乘方求廉法。一次同余方程组解法发轫于《孙子算经》物不知数问。但数值较简单。天文学家制定历法计算上元积年时也要解同余方程组,但“历家虽用,用而不知”,甚至误认为是方程术。[4]秦九韶总结了历代关于上元积年的计算,发展了孙子算法,归纳出大衍总数术及大衍求一术,并对问题给出的元数不两两互素的情况给出了不同的处理方法,形成了比较系统的同余方程组理论,超前其他民族五六个世纪。
赵爽、刘徽等数学家经常提到的“引而申之”“触类而长之”等方法,源于《周易》;刘徽还说到“告往知来”“举一反三”,也是这种意思。它们主要指类比的思维方法,是通类、类以合类的另一方面。今有术本来是处理谷物交换问题的方法,刘徽认为:“诚能分诡数之纷杂,通彼此之否塞,因物成率,审辨名分,平其偏颇,齐其参差,则终无不归于此术也。”[1]这就是说,一个数学问题,只要能找出诸因素的率关系,通过齐同,都可以化为今有术求解,这就是举一反三的类比过程。刘徽之前,人们已从分数加减运算中总结出齐同术,即把各分数化成同一分母,又使分数的分子与分母相齐。刘徽发现率关系与分数的分子、分母的关系相类似,因此,在率关系中可以施用齐同术。同一问题中若有几个率关系,要找出联结诸率关系的中率,同其中率,再使其他元素的率与之相齐,则可使诸率悉通。如甲∶乙=a∶b1,乙∶丙=b2∶c,同乙之率为b1b2,使甲、丙之率与乙相齐,分别为ab2,b1c,则甲∶乙∶丙=ab2∶b1b2∶b1c或甲∶丙=ab2∶b1c,直接应用今有术。刘徽进一步指出:“凡率错互不通者,皆积齐同用之。放此,虽四、五转不异也。”[1]刘徽解各种算术问题及方程术、方程新术中都用到齐同术。刘徽说:“乘以散之,约以聚之,齐同以通之,此其筭之纲纪乎?”[1]齐同术成为解决计算问题的有力工具。刘徽在注《九章算术》方程章牛羊直金问时创造了互乘相消法,然后指出:“以小推大,虽四五行不异也。”[1]可见,类比推理是中国古代数学家扩充数学知识的重要方法。
类比甚至成为中国古代数学著述的体倒,叫作比类。南宋杨辉详解《九章算术》的一种内容叫比类,所谓“僭比类题以通俗务”。[5]还著《田亩比类乘除捷法》,明吴敬著《九章算法比类大全》。北宋沈括以刍童比类刍童形垛积,认为两者形状相类,但垛积中间有间隙,若把垛积长、宽、高的个数看作尺寸数,用《九章算术》的刍童体积公式求垛积的个数则偏小。他经过反复思考,得出刍童垛个数比刍童体积尺数多![]() (c-a),其中a,c为垛积上、下宽的个数,n为层数。[6]杨辉又用方锥垛、方垛、三角垛、刍甍垛分别比类于方锥(阳马同)、方亭、鳖腝、刍甍,求出它们的垛积公式。这都是二阶等差级数求和问题,是中国数学史上的一个新课题。
(c-a),其中a,c为垛积上、下宽的个数,n为层数。[6]杨辉又用方锥垛、方垛、三角垛、刍甍垛分别比类于方锥(阳马同)、方亭、鳖腝、刍甍,求出它们的垛积公式。这都是二阶等差级数求和问题,是中国数学史上的一个新课题。
比类的另一种形式就是用对象不同而数学方法一致的问题来比类。如《九章算术》竹高折地问是已知勾与股弦和求股的问题,贾宪总结出股弦和与勾求股法,[5]杨辉认为,若长方田已知其宽及对角线与长之和,求田面积,则可用这种方法,因之进行比类。[7]
利用对称性是进行类比的一种重要方式。刘徽在分析竹高折地问的方法之后说:“此术与系索之类更相反覆也。”[1]盖系索之类是已知勾与股弦差求股、弦的问题:![]() ,竹高折地问是已知勾与股弦和求股、弦的问题:
,竹高折地问是已知勾与股弦和求股、弦的问题:![]() ,两者具有对称性。
,两者具有对称性。
洞渊、李冶则更灵活地运用了这种方法。九容公式中勾上容圆径为d=![]() ,股上容圆径便为d=
,股上容圆径便为d=![]() ;同样,勾外容圆径为d=
;同样,勾外容圆径为d=![]() ,股外容圆径便为d=
,股外容圆径便为d=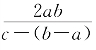 ;等等。在“识别杂记”中有若干关于圆城的对偶性命题。这样,只要确定一个命题为真,则其对偶性命题必为真。甚至,《测圆海镜》的卷三与卷四、卷五与卷六的题目也是对偶关系,知道了卷三、卷五的题目的解法,则卷四、卷六中相应题目便可依法演算。如卷三第5问“或问乙出南门,东行七十二步而止;甲出西门,南行四百八十步,望乙与城参相直。问荅同前。”所谓“问荅同前”即“问径几里”,下同。[7]如图,以直角顶表示该勾股形,b金即勾股形金山天之股,依次类推。用天元术列出开方式:
;等等。在“识别杂记”中有若干关于圆城的对偶性命题。这样,只要确定一个命题为真,则其对偶性命题必为真。甚至,《测圆海镜》的卷三与卷四、卷五与卷六的题目也是对偶关系,知道了卷三、卷五的题目的解法,则卷四、卷六中相应题目便可依法演算。如卷三第5问“或问乙出南门,东行七十二步而止;甲出西门,南行四百八十步,望乙与城参相直。问荅同前。”所谓“问荅同前”即“问径几里”,下同。[7]如图,以直角顶表示该勾股形,b金即勾股形金山天之股,依次类推。用天元术列出开方式:
x3-(b金-2a南)x2+a2南x+a2南b金=0
而卷四第5问:“或问乙出东门,南行三十步而止;甲出北门,东行二百步,望见乙与城参相直。问荅同前。”[7]其开方式为:
x3-(a北-2b东)x2+b2东x+a北b2东=0
两者形式完全相同,[8]其原因在于b金与a北,a南与b东的位置相应。
通类、类以合类的另一含义是对数学知识进行分类。这是数学知识积累到一定程度的必然结果。先秦将数学知识分成九个部分,即九数:方田、粟米、差分、少广、商功、均输、方程、盈不足、旁要,[9]后来发展成《九章算术》,其中旁要变成了勾股。南宋秦九韶在《数书九章》中将他的数学知识分成大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易九类。这些分类有的按应用,有的按方法,不尽合理。刘徽力图按数学方法分类,比如他指出《九章算术》均输章凫雁、长安至齐、成瓦、矫矢、假田、程耕、五渠共池诸问都是同工共作类问题。勾股章引葭赴岸、系索、倚木于垣、勾股锯圆材、开门去阃诸问都是由勾及股弦差求股、弦的问题。刘徽还对数学方法分了不同的级别,如衰分术等术在《九章算术》中与今有术并列,而刘徽认为今有术是都术,衰分术等都可归结为今有术,[1]实际上在今有术与衰分术等之间建立了种属关系。然而,刘徽没有试图从形式上改变《九章算术》的格局。南宋杨辉在详解《九章算术》之后撰《九章纂类》,将《九章算术》的数学知识按方法分成乘除、互换、合率、分率、衰分、叠积、盈不足、方程、勾股九类,尽管恪守“九”字,并且分类、命名亦有不合理之处,但打破《九章算术》的沿习千余年的格局,是个进步。
通类、类以合类的又一体现就是从一般到特殊的演译过程,这就是一般公式在具体数学问题中的应用。《九章算术》今有术、衰分术、返衰术、少广术、方程术等的应用典型地反映了这种过程。这几部分的格式是:总术、例题及答案和应用总术的具体术文。今有术有31个应用题;衰分术有7个,返衰术有2个,少广术有11个,方程术有18个。以衰分术及一个应用题为例:
衰分术曰:各置列衰,副并为法,以所分乘未并者各自为实,实如法而一。
其例题的第2问是:
今有牛、马、羊食人苗。苗主责之粟五斗。羊主曰:“我羊食半马。”马主曰:“我马食半牛。”今欲衰偿之,问:各出几何?(答案略)
术曰:置牛四、马二、羊一,各自为列衰,副并为法。以五斗乘未并者各自为实。实如法得一斗。[1]
同样,大衍总数术及其大衍求一术是秦九韶提出的一次同余方程组的一般解法,然后被应用于蓍卦发微、古历会积、推计土功、推额库钱、分粜推原、程行计地、程行相及、积尺寻源、余米推数及治历演纪等10个具体问题,也是一个演绎过程。中国古算中,这类例子还有很多。
三
说中国古代数学没有理论,主要的论据是没有推理。这种论据对不对呢?翻开刘徽《九章算术注》和某些宋元著作,自然会得出否定的结论。刘徽注《九章算术》的宗旨是“析理以辞,解体用图”。图已佚,我们分析他的辞。《墨子·大取》说:“夫辞,以故生,以理长,以类行者也。”[10]刘徽析理以辞,是用辞阐明数学上的术即公式、解法以及一些原理为什么是真理,实际上是用辞建立理、类、故的联系。据统计,刘徽《九章算术注》用了219个“故”字,其中训旧的只有3个;训原因、是以,用于推理、定义的216个,占98.63%,[11]在古代典籍中,可与《墨子》相媲美。另外还有一些训“故”的“是以”等词。这些“故”“是以”,有一部分用于与数学有关的议论,但大多数用于数学推理。以类求故,由故成理,这种归纳的过程,我们上面谈到了一些。此处着重说明以故求理,由理知类的演绎过程。数学著作,不是逻辑教程,其推理过程的阐述不可能像逻辑教程那样完整,其间有省略,甚或顺序的颠倒。但是,只要不带成见,便会从中得出应有的结论。比如,刘徽在《九章算术》方田术“广从步数相乘得积步”[1]下注曰:“此积谓田幂。凡广从相乘谓之幂。”[1]由于注书行文的方便,先列出经文作小前提,再给出结论,最后提出幂的定义作为大前提。其推理过程应该是:凡广从相乘谓之幂。此积为广从相乘,故此积谓田幂(这里还用了附性法)。显然这是一个三段推理。[12]刘徽把幂看作积之一种,积是属,包括二数之积、三数之积等,而幂专指两数之积。李淳风等既不懂积、幂之区别,一会说“积幂义同”,又看不懂积幂的联系,一会说“二者全殊”,[1]足见其不顾事实及逻辑水平之低下。有的同志以李淳风等对刘徽的曲解为根据指责刘徽是不合适的。
又如刘徽在注方程术的直除法时说:“为术之意,令少行减多行,反复相减,则头位必先尽。上无一位则此行亦阙一物矣。然而举率以相减,不害余数之课也。若消去头位,则下去一物之实。如是直令左右行相减,审其正负,则可得而知。”[1]这个推理实际上可以简化成:举率以相减是不害余数之课的。直除法是举率相减,故直除法不害余数之课。大前提是全称否定判断,小前提是单称肯定判断,结论是单称否定判断。这是一个三段论第一格推理。
作为数学著作,刘徽注的关系推理俯拾皆是,还有假言推理、联言推理等演绎推理。[1]
刘徽还使用了其他演绎推理。笔者无意用现代逻辑模式去削足适履,硬套中国古典数学。各个不同的文化传统,各个不同的时代,人们的思维方式固然会有不同特点,但是,作为人类的思维,必然遵循共同的思维规律。我们的祖先也不会例外。这已为众多的中国逻辑史的研究专著所一再证明。中国古典数学以算法研究为主。同样有命题的确定与推理的严谨等这样一些数学的共同特性,不仅不会例外于人类共同的思维规律,反而会比其他著作乃至哲学著作表现出更强的逻辑性。上面所举的例子已经证明了这一点。因此,我们的研究不应着言于中国古典数学有没有逻辑(非逻辑性的直觉在任何学科、任何文化传统中都存在),而应探讨它的逻辑思维的方式及其有什么不同于其他传统的特点。
由于上面提到的推理的前提是真确的,因此它们实际上都是数学证明。中国古代数学著作,尤其是刘徽注中,有若干成功的复杂的数学证明,谨举几个例子。《九章算术》勾股章“户高多于广”问[1]是一个已知弦c与勾股差b-a求勾a、股b的问题,刘徽将公式简化成:
刘徽的证明是:
弦幂适满万寸。倍之,减句股差幂,开方除之。其所得即高广并数。以差减并而半之,即户广;加相多之数,即户高也。[1](https://www.xing528.com)
用符号写出,就是:∵c2=a2+b2,2c2=2a2+2b2,∴2c2-(b-a)2=2a2+2b2-(b-a)2=(a+b)2,∴![]() =a+b。而a=
=a+b。而a=![]() [(a+b)-(b-a)],b=
[(a+b)-(b-a)],b=![]() [(a+b)+(b-a)],∴a=
[(a+b)+(b-a)],∴a=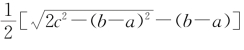 ,b=
,b=![]() 。证毕。这是一个从予到求的综合法演绎证明。其中“弦幂适满万寸”是没有必要的,大约是保留的归纳论证的痕迹。
。证毕。这是一个从予到求的综合法演绎证明。其中“弦幂适满万寸”是没有必要的,大约是保留的归纳论证的痕迹。
又如圆面积公式S=![]() Lr的证明,也是一个从予到求的综合法证明[2]。
Lr的证明,也是一个从予到求的综合法证明[2]。
刘徽有的证明则采用了以分析法为主,综合法为辅的方式。上面已经指出,刘徽证明了棊验法无法证明阳马、鳖腝的一般体积公式。为了彻底解决这个问题,刘徽首先提出了刘徽原理。他证明刘徽原理的过程是综合法,而综合中又有分析过程[3]。
圆面积公式和阳马、鳖腝体积公式的证明中含有明显的无穷小分割思想和极限过程。刘徽说:“数而求穷之者,谓以情推,不用筹算。”过去,否定中国古代数学有理论的学者没有搞懂这两个证明,近来说中国古代数学具有非逻辑性特征的同志也回避了这两个证明。
刘徽、王孝通都提出了方程的推导过程。金元数学家更创造了设未知数列方程的统一方法天元术。这些推导实际上都是演译过程。上面已经指出,李冶《测圆海镜》诸算题所需要的定理、公式大都在“识别杂记”中给出。谨以第七卷第18问为例。题目是:
或问:甲、丙二人俱在西北隅,甲向东行,丙向南行;又乙出南门东行,丁出东门南行,各不知步数而立。四人遥相望见,悉与城参相直。既而相会,甲云“我与乙共行了三百九十二步”,丙云“我与丁共行了六百三十步”。问荅同前。[10]
如前图所示,此已知甲行乾地即a乾,丙行乾天即b乾,乙行南月即a南,丁行东山即b东,天、月、山、地在一直线上且与圆相切,已知a乾+a南及b乾+b东,求圆径即山金。立天元一为圆城径,即山金为x。由识别杂记得a乾+a南-![]() =c泉,b乾+b东-
=c泉,b乾+b东-![]() =c金,而a2泉=c2泉-x2=(a乾+a东-
=c金,而a2泉=c2泉-x2=(a乾+a东-![]() )2-x2=(392-
)2-x2=(392-![]() )2-x2=-0.75x2-392x+153 664,b2金=c2金-x2=(b乾+b东-
)2-x2=-0.75x2-392x+153 664,b2金=c2金-x2=(b乾+b东-![]() )2-x2=(630-
)2-x2=(630-![]() )2-x2=0.75x2-630x+396 900。由诸杂名目圆径公式黄广股黄长勾相乘为径幂,即x2=a泉×b金,∴x4=a2泉×b2金。而a2泉×b2金=(-0.75x2-392x+153 644)(0.75x2-630x+396 900)=0.5 625x4+766.5x3-165 963x2-252 393 120x+60 989 241 600。与同数x4相消,得-0.4 375x4+766.5x3-165 963x2-252 393 120x+60 989 241 600=0。用不到多少解释。这个四次方程的推导是一个演绎过程。
)2-x2=0.75x2-630x+396 900。由诸杂名目圆径公式黄广股黄长勾相乘为径幂,即x2=a泉×b金,∴x4=a2泉×b2金。而a2泉×b2金=(-0.75x2-392x+153 644)(0.75x2-630x+396 900)=0.5 625x4+766.5x3-165 963x2-252 393 120x+60 989 241 600。与同数x4相消,得-0.4 375x4+766.5x3-165 963x2-252 393 120x+60 989 241 600=0。用不到多少解释。这个四次方程的推导是一个演绎过程。
四
古希腊各学派重视数学与自然科学的研究,并热衷于科学问题的互相辩难。他们的数学著作追求明确的定义,严谨的推理,力图自成一个不怕别人诘难的和谐的公理化体系。[13]中国古代数学与此不同,读者不能与作者处于辩难的地位而是必须与作者共处于一个和谐的体系中。这首先表现在数学概念没有明确的定义,而是靠约定俗成。《九章算术》的数学概念,不管是方田、广、从、阳马、方锥等具体概念,还是并、减、乘、约、率、如、衰分、同、方程、直除等抽象概念,其含义都靠约定俗成,而没有明确界定。后来刘徽、秦九韶、李冶对许多概念作了定义,但对相当多的概念仍靠约定俗成确定其含义。同样,对数学运算、数学推理中所使用的许多原则,并不必列出,却心照不宣地应用,如等量加(减)等量,其和(差)相等,一个图形平移或旋转不改变其面积或体积,一个图形被分成若干部分,所有部分的面积或体积总和等于其总面积或体积等等原理,都未作任何描述,而实际上成为大家必须共同遵守的准则。
同时,中国古代数学著作的一些题目的设问条件有时并不完备,读者必须按照作者的未明言的思路去理解、补充某些条件。如其率术的例题的格式是:
今有出钱若干(A),买物若干(B),欲其贵贱(某单位)率之,问:各几何?[1]
设贱价单价x钱,买u单位;贵价单价y钱,买v单位,按题设只能列出一个四元不定方程:
ux+vy=A
u+v=B
其中既未说求整数解,也未说每单位的价格差1钱。然而这些问题的总术是:
其率术曰:各置所买石、钧、斤、两以为法,以所率乘钱数为实,实如法而一。不满法者,反以实减法,法贱实贵。[1]
这种方法用现代符号表示出来便是:
实际上是求满足y-x=1的整数解。
即使是辩难之风盛行的魏晋,刘徽《九章算术注》中有的文字也有歧义。如上面提到的阳马、鳖腝体积公式证明中谈到赤黑堑堵的拼合时,刘徽说:“令赤黑堑堵各自适当一方。”[1]就字面而言,既可以是两赤堑堵相拚合、两黑堑堵相拚合,亦可以是一赤堑堵与一黑堑堵相拚合。到底哪种方式对呢?由于两赤堑堵或两黑堑堵只有在长、宽、高相等时才能合成方体,在长、宽、高不等的情况都无法合成一方体,而前者用棊验法已经解决,不必作如此复杂的分割;此段的本意是解决“方随棊改”的长、宽、高不等的情况,而此种情况下只有一赤堑堵一黑堑堵相拚合才能得到成方体。因此只能采取一赤堑堵一黑堑堵相拚合。就是说,必须择善而从。
又如,刘徽提出的刍童的一个新体积公式:“又可令上下广袤互相乘而半之,上下广袤又各自乘,并,以高乘之,三而一,即得也。”[1]就字面而言,既可写成
又可写成
其中a1,b1是上底宽、长,a2,b2是下底宽、长,h是高。择善而从,只能取前一种方式。显然,这样的著作,其读者不能是持白马非马之类命题的诡辩论者,而是必须与作者配合默契,按照作者的意图理解问题,共处于一个和谐的体系。不了解中国古代数学的这一特征,就无法正确理解原著,或者认为原文有误,硬去作并非必要的校改,替古人修辞。
中国数学的这一特点总的说来不利于更深入更严格地讨论问题,不利于数学的发展。但是事物的利弊总是相辅相成的,刘徽没有像古希腊数学家那样陷入实无限与潜无限的争论,也不考虑![]() 与1是否有公度的问题,没有涉及在古希腊引起数学危机,甚至引起改变数学发展方向,摒弃极限思想的悖论,因此才能在证明中明确使用无穷小分割和极限思想,才能提出开方不尽以十进分数逼近无理根的“求微数”思想,把中国数学的理论和计算能力提高到一个新的阶段。
与1是否有公度的问题,没有涉及在古希腊引起数学危机,甚至引起改变数学发展方向,摒弃极限思想的悖论,因此才能在证明中明确使用无穷小分割和极限思想,才能提出开方不尽以十进分数逼近无理根的“求微数”思想,把中国数学的理论和计算能力提高到一个新的阶段。
参考文献
[1]郭书春汇校.九章算术.沈阳:辽宁教育出版社,1990.*郭书春汇校.九章筭术新校.合肥:中国科学技术大学出版社,2014.
[2][唐]魏征,等.隋书·律历志.北京:中华书局,1973.
[3]钱宝琮校点.周髀算经.钱宝琮校点.算经十书.北京:中华书局,1963.*郭书春、刘钝等主编.李俨钱宝琮科学史全集(4).沈阳:辽宁教育出版社,1998.
[4][宋]秦九韶.数书九章.宜稼堂丛书本.郭书春主编.中国科学技术典籍通汇·数学卷(1).郑州:河南教育出版社,1993.
[5][宋]杨辉.详解九章算法.宜稼堂丛书本,1843.郭书春主编.中国科学技术典籍通汇·数学卷(1).郑州:河南教育出版社,1993.
[6][宋]沈括.梦溪笔谈.北京:文物出版社影印元刊本,1975.
[7][元]李冶.测圆海镜.知不足斋丛书本,1798.郭书春主编.中国科学技术典籍通汇·数学卷(1).郑州:河南教育出版社,1993.
[8][法]K.Chemla(林力娜).Equations with Genenal C 0eflicients in the〈测圆海镜〉.
[9][汉]郑玄注.周礼.阮元校.十三经注疏.北京:中华书局,1979.
[10]孙诒让.墨子间诂.北京:中华书局,1954.
[11]郭书春.古代世界数学泰斗刘徽.济南:山东科学技术出版社,1992.繁体字修订本.台北:明文书局,1995.*再修订本.山东科学技术出版社,2013.
[12]郭书春.刘徽《九章算术注》中的定义及演绎逻辑试析.自然科学史研究,1983,2(3).
[13][美]M.克莱因.古今数学思想.上海:上海科学技术出版社,1979.
【注释】
[1]*关于关系推理、假言推理等的例子,请参见本文集《刘徽〈九章算术注〉中的定义及演绎逻辑试析》,此处删去。
[2]*关于这个证明的方法,请参看本文集的《刘徽的极限理论》,此处删去。
[3]*关于这个证明的方法,请参看本文集的《刘徽的体积理论》,此处删去。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




