古代中国数学哲学问题探究

①本文原载《自然辩证法研究》第4卷第3期，1988。今选取前三节。其第四节与收入本文集的《刘徽〈九章算术注〉中的定义及演绎逻辑试析》多所重复，删去。

中国古代数学从公元前1世纪到14世纪初取得到了若干重大成就，成为当时世界数学研究最发达的地区之一。伴随着这些成就，数学家、哲学家们先后提出了若干深邃的数学哲理。由于此后中国数学衰落，更由于20世纪初年以后中国古代数学传统中断，我国现在的数学工作者（包括大、中、小学教师和科研工作者）受的是现代数学教育，大多对中国古算知之甚少。中国哲学史家大多既不懂现代数学，又不懂中国古算，许多哲学史著作都回避中国古算中的方法论、逻辑学等问题。有的著作力图探讨这类问题，往往失之偏颇，甚或发生谬误。中国数学史学科的奠基者李俨、钱宝琮等前辈，他们当时的主要任务是研究中国古代数学的成就，理出其发展的脉络，尚无暇顾及其中的哲学问题。钱老晚年开始注意这个问题，发表了几篇很有分量的论文[1][2][3]。可惜由于十年浩劫，这种研究中断了。国外的中国数学史家如三上义夫、李约瑟、尤什凯维奇等，对中国古代数学成就一般说来持比较客观、公正的态度。然而他们普遍认为中国古代的数学成就只是经验的总结，没有理论[4]。很不幸，由于种种原因，李约瑟等人的某些不恰当的观点在国内流传很广，甚至在许多人看来，比中国学者的论述更可信。本文想就几个问题谈一些看法，以期抛砖引玉。

一

由于先秦诸子对数学和自然科学普遍不重视，当时对数学的性质、对象、方法和作用的讨论并不多，后来也未达到像古希腊那样深入的程度。

《老子》说：“道生一，一生二，二生三，三生万物。”[5]这与古希腊毕达哥拉斯学派的主张相近。毕氏学派认为，“万物的始基是‘一元’。从‘一元’产生出‘二元’”，进而“产生出各种数目；从数目产生出点，从点产生出线，从线产生出平面，从平面产生出立体，从立体产生出感觉所及的一切物体，产生出四种元素：水、火，土、空气”，进而产生了整个世界。总之，“数目的基本元素就是一切存在物的基本元素。”[6]“宇宙的组织在其规定中是数及其关系的和谐体系。”[7]老子的话，他自己没有详细阐释，后来的道家及其他学派也没有进一步分析。他主张“道生一”与毕氏学派有所不同，然而主张从“一”派生出万物来，却是相同的。

南北朝时成书的《孙子算经》序言中说：“夫筭者，天地之经纬，群生之元首，五常之本末，阴阳之父母，星辰之建号，三光之表里，五行之准平，四时之终始，万物之祖宗，六艺之纲纪。”[8]这里把算学看成从精神到物质的一切事物的本源，是“万物皆数”思想的一种反映，不过就《孙子算经》的题目来看，并没有这方面的内容。

总的来说，在中国古代由于对数学没能重视到应有的程度，“万物皆数”的思想在传统数学中影响不大。

对数学的作用，也表现了不同的分野。《孙子算经》序言中认为数学从天道到地理，从人事到神祗，从道德到性命，无所不能，然而《孙子算经》的题目除一问推算生男生女纯属无稽之谈外，全来自于实际问题，并未背离中国古算理论联系实际的传统。13世纪秦九韶认为数学“大则可以通神明，顺性命，小则可以经世务，类万物”，认为“数与道非二本”。然而秦九韶通过自己的数学实践认识到“所谓通神明，顺性命，固肤末于见。若其小者，窃尝设为问答以拟于用”，[9]撰《数书九章》，设计了81个问题，取得了十分重大的成果。

刘徽关于数学的作用的看法是比较正确的。他说，数学虽然只有九个部分（即九数），其能却能“穷纤入微，探测无方”[10]，既肯定了数学的作用，又未陷入神秘主义，这种看法反映了从《九章算术》以来我国数学的主流。

至于数学知识的来源，以刘徽、李冶为代表，认为数学来源于客观世界的空间形式和数量关系。刘徽在阐明数学并不神秘时说：“至于以法相传，亦犹规矩度量可得而共，非特难为也。”[10]规、矩是古代画圆、画方的工具，这里代表空间形式，度量就是度、量、衡，这里代表数量关系。刘徽的话不仅说明了数学的对象和来源，而且体现了我国古代数学融几何、代数于一体的特点。13世纪李冶发展了刘徽的思想，他说：“彼其冥冥之中，固有昭昭者存。夫昭昭者，其自然之数也。非自然之数，其自然之理也。”显然，他认为数学就是自然之数、自然之理的反映，“数一出于自然。”[11]刘徽和李冶的这些观点在数学本体论上实际上是认为数学是人们对客观事物的空间形式和数量关系抽象思维的结果，它是不能独立于客观事物而独立存在的。

当然，在中国古代数学界也存在着数学神创的观点。古代有所谓“河出图、洛出书”的神话[12]，到13世纪秦九韶提出“河图洛书闿发秘奥”的看法，[9]这种看法对后世有一定影响，不过就是秦九韶也认为“数术之传，以实为体”。他提出的81个问题绝大多数比他以前和同时的著作更加密切联系当时的实际需要，还是复归到《九章算术》的传统和刘徽的观点。

二

中国古代数学以定量研究为主，以计算为中心，采取以术文统率应用问题的形式，代数学特别发达，长于算法理论的研究，形成了与古希腊以欧几里得《几何原本》为代表的公理化体系迥然不同的风格。之所以形成如此不同的风格，除其他原因外还有深刻的哲学背景。

古希腊的哲学家大都是科学家，他们精通数学，或者就是有建树的数学家，因此他们忽视数学的实际应用，却长于数学知识的理论概括。而中国数学起步的先秦，诸子百家只注重治国平天下和伦理道德的研究，普遍地对数学和其他科学技术不重视，即使是最重视科学的墨家，其数学知识也难以与古希腊的学者相比，数学知识多掌握在文化层次较低的阶层中，这就造成中国数学起步的时候，长于实际应用，却与理论研究脱节，忽视理论概括。另一方面，中国有当时世界上最先进的十进位值制记数法和最先进的计算工具算筹，使人类的计算才能在中国比较容易得到充分发挥。

毕达哥拉斯学派对和1没有公度这一事实的发现，导致了数学的第一次危机。当时人们无法解释这一悖论，对数量关系望而生畏。此后希腊人的数学研究往往避开数量关系，专注于空间形式，[13]因此几何学特别发达。中国古代没有提出任何悖论，可以无所顾忌地进行数字之间的运算。《九章算术》开方术曾提出“若开之不尽者为不可”，这本来打开了通向“无理数”概念的大门，可接着又提出了“当以面命之”，[10]以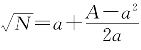作为根的近似值，随即关上了深入研究“不可开”的大门。刘徽认为《九章算术》求近似值的方法不准确，提出了求微数即十进分数的方法。他说：“不以面命之，加定法如前，求其微数。微数无名者以为分子，其一退以十为母，其再退以百为母，退之弥下，其分弥细，则朱幂虽有所弃之数，不足言之也。”[10]刘徽求微数的意义十分重大，它不仅开创了宋元时代十进小数的先河，使我国成为世界上最先使用十进小数的国家，而且是圆周率计算的基础。倘无求微数的方法，且不说祖冲之将圆周率精确到八位数字是不可能的，就是刘徽精确到也不可能。刘徽通过求微数逼近无理根的作法来源于他对数的认识。《老子》说：“无名天地之始，有名万物之母。”刘徽的同代人王弼说：“一，数之始而物之极也。”[5]刘徽受此影响，提出：“少者多之始，一者数之母。”[10]这就把任何数都看成与一有公度的。因此，可以自由地求无理根的近似值而不必考虑哲学上的困难。许多事物往往是利弊相辅相成。刘徽求微数的意义固然重大，却永远关闭了在中国独立发现无理数的大门。

负数的引入是数系的一次大扩充。在欧洲直到16世纪甚至18、19世纪还有人对它的合理性提出怀疑。如19世纪德摩甘说：“0-a和同样是不可思议的。”[14]19世纪在欧洲不可思议的事，在公元前2、3世纪的中国却未遇到任何麻烦。《九章算术》在线性方程组消元时就引入了负数，提出了“正负术”即正负数加减法则，刘徽进而提出了正负数的定义：“今两筭得失相反，要令正负以名之。”[10]并提出运算中取哪个数为正哪个数为负都是相对的，可以由计算的方便而决定。

三

对无限的认识，是数学哲学的重要问题。古希腊的亚里士多德第一次区分了实无限和潜无限[14]。潜无限就是指“分割的过程永远不会告终。”[6]他认为“只有潜能上的无限”，“不会有现实的无限。”[7]中国古代没有潜无限、实无限的名称，却实际上存在着这种区别。名家的“一尺之捶，日取其半，万世不竭”[15]的命题，就是认为分割永远有剩余，这实际上是一种“潜无限”的观点。而墨家“端”及其分割可以达到“不可”[16]的境地，则是一种“实无限”的观点。

在中国，刘徽第一次把无穷小分析应用于数学证明。他的思想是墨家分割思想的承袭和发展。为了说明这个问题，我们分析一下他关于圆面积公式S=Lr的证明，其中S，L，r分别是圆的面积、周长和半径。刘徽从圆内接正六边形开始割圆，依次得到12，24，……边形，它们与圆面积之差越来越小，刘徽说：“割之又割，以至于不可割，则与圆周合体而无所失矣。”[10]这里的“不可割”与墨家的“不可”一脉相承，而边数无限的正多边形与圆周合而而为一体现了刘徽无穷小量的实无限性。接着刘徽指出，正多边形每边与圆周之间有一余径，余径乘边长加到多边形面积上，则大于圆面积。在与圆周合体时，则“表无余径。表无余径，则幂不外出矣”。最后刘徽说：“以一面乘半径，觚而裁之，每辄自倍，故以半周乘半径而为圆幂。”[10]将与圆合体的正多边形分割成无穷多个以圆心为顶点以每边为底的小三角形，计算它们的面积，求其和，即证明了圆面积公式。显然，刘徽无限分割得到的这个正无穷多边形既与圆周合体，又保持了正多边形的特性，其每边既是零，又是非零，体现了无穷小量的潜无限性。总之，刘徽的无穷小量体现了它的过程与终结的辩证统一，体现了潜无限与实无限的辩证统一。刘徽在证明四面体（鳖腝）体积时的无穷分割中提出的“至细曰微，微则无形”[10]也是一种潜无穷与实无穷统一的思想。

不言而喻，刘徽关于无穷小量的思想比古希腊的同类思想要高出一筹。由于无法解释芝诺悖论，希腊数学家不得不把无限排斥在自己的推理之外。如在穷竭法中，尽管从理论上讲所进行的分割可以无限继续下去，然而在用于数学证明时，却从未使用过无穷小量和极限思想，分割中总有一个剩余，包括数学大师阿基米德在内，都用双重归谬法而不是极限思想证明已知的命题。[13][14]与刘徽类似方法证明圆面积公式的是尼古拉斯（1401—1464），他把圆定义为边数最多的多边形，[17]其后的分割方法与刘徽完全一致。他用定义回避了刘徽的两个极限过程。(www.xing528.com)

参考文献

[1]钱宝琮，杜石然.试论中国古代数学的逻辑思想.光明日报.1961-05-29.

[2]钱宝琮.宋元时期数学与道学的关系.宋元数学史论文集，北京：科学出版社，1966.又：钱宝琮科学史论文选集.北京：科学出版社，1983.*郭书春、刘钝等主编.李俨钱宝琮科学史全集（9）.沈阳：辽宁教育出版社，1998.

[3]钱宝琮.《九章算术》及其刘徽注与哲学思想的关系.钱宝琮科学史论文选集.北京：科学出版社，1983.*郭书春、刘钝等主编.李俨钱宝琮科学史全集（9）.沈阳：辽宁教育出版社，1998.

[4][英]Needham J.（李约瑟）.中国科学技术史，第3卷.北京：科学出版社，1978：337～338.

[5][三国魏]王弼.老子道德经注释.北京：中华书局.

[6]古希腊罗马哲学.北京：商务印书馆，1961.

[7][希]亚里士多德.形而上学.北京：商务印书馆，1959.

[8]孙子筭经.宋刻算经六种.北京：文物出版社，1980.

[9][宋]秦九韶.数书九章.宜稼堂丛书本，1842.*郭书春主编.中国科学技术典籍通汇·数学卷（1）.郑州：河南教育出版社，1993.

[10]郭书春.汇校《九章算术》.沈阳：辽宁教育出版社.1990.*郭书春汇校.九章筭术新校附录.合肥：中国科学技术大学出版社，2014.

[11][元]李冶.测圆海镜.知不足斋丛书本，1798.*郭书春主编.中国科学技术典籍通汇·数学卷（1）.郑州：河南教育出版社，1993.

[12][汉]郑玄.周礼注.阮元校.十三经注疏.北京：中华书局影印，1979.

[13][美]M.克莱因，古今数学思想.上海：上海科学技术出版社，1978.

[14]夏基松，郑毓信.西方数学哲学.北京：人民出版社，1986.

[15]庄子.郭庆藩.庄子集释.北京：中华书局，1961.

[16]孙诒让.墨子间诂.北京：中华书局，1954.

[17][美]波耶.微积分概念史.上海：上海人民出版社，1976.