1.积分
在《九章筭术》开方问题中没有使用“积分”的概念,而刘徽关于开平方问题的注中用到“积分”的地方有2处。《九章筭术》少广章开方术的刘徽注云:
术或有以借筭加定法而命分者,虽粗相近,不可用也。凡开积为方,方之自乘当还复其积分。令不加借筭而命分,则常微少;其加借筭而命分,则又微多。
原来,为了求根,在刘徽之前,或者以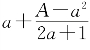 作为近似值,或者以
作为近似值,或者以![]() 作为近似值,刘徽认为都不准确。为什么呢?因为对一个数开方,那么它的根自乘应该恢复原数。如果以一个分数表示根,那么根的自乘应该恢复原数的积分。这里的积分显然是面积的分数的积累。可是
作为近似值,刘徽认为都不准确。为什么呢?因为对一个数开方,那么它的根自乘应该恢复原数。如果以一个分数表示根,那么根的自乘应该恢复原数的积分。这里的积分显然是面积的分数的积累。可是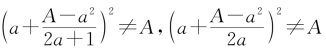 ,而是a+
,而是a+![]() “微少”,a+
“微少”,a+ “微多”,即
“微多”,即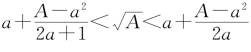 。
。
《九章筭术》勾股章今有邑方不知大小问的刘徽注云:
令二出门相乘,故为半方邑自乘,居一隅之积分。因而四之,即得四隅之积分。故为实,开方除,即邑方也。
这里的积分的涵义与上相同,也是面积的分数的积累。
2.积步、积里
为了进一步理解《九章筭术》及其刘徽注中“积分”的涵义,我们分析一下其中与“积分”同类的积步、积里等概念。同样,在下面提到的某些术文和例题,秦简《数》、汉简《筭数书》中也有,但是没有用到积步、积里等术语。
《九章筭术》在方田章有4次使用“积步”,依次是:
方田术曰:广从步数相乘得积步。
圆田术云:
半周半径相乘得积步。
环田术云:
并中、外周而半之,以径乘之,为积步。
环田术提出:(https://www.xing528.com)
密率术曰:置中、外周步数,分母、子各居其下。母互乘子,通全步,内分子。以中周减外周,余半之,以益中周。径亦通分内子,以乘周为密实。分母相乘为法。除之为积步,余,积步之分。以亩法除之,即亩数也。
刘徽用到“积步”也有4次。圭田术刘徽注云:
亦可半正从以乘广。按半广乘从,以取中平之数,故广从相乘为积步。
刘徽注又云:
按:半周为从,半径为广,故广从相乘为积步也。
环田密率术刘徽注:
按:此术,并中、外周步数于上,分母、子于下。母互乘子者,为中、外周俱有分,故以互乘齐其子。母相乘同其母。子齐母同,故通全步,内分子。“半之”知,以盈补虚,得中平之周。周则为从,径则为广,故广、从相乘而得其积。既合分母,还须分母出之。故令周、径分母相乘而连除之,即得积步。
少广术刘徽注:
一亩积步为实。
这里的积步都是平方步之积,也就是平方步的积累。因此,积步是《九章筭术》提出的表示面积的概念,也可以作为面积的单位,即步之积。将1步长的线段在平面上积累起来,长a步,就是a积步,常简称为a步,步即今之平方步。因此古代之步,视不同情况,有时指今之步,有时指步2。
《九章筭术》还使用了“积里”的概念。其方田章里田术云:
里田术曰:广从里数相乘得积里。
刘徽注云:
按:此术广从里数相乘得积里。
积里是平方里的积累。与积步类似,都是面积问题中的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




