数学史自选集：关于长度问题中的积分

秦简《数》《筭书》与汉简《筭数书》《九章筭术》都有少广术。《筭数书》与《九章筭术》的少广术都使用了术语“积分”，而《数》《筭书》中则没有。《筭数书》的少广术是：

求少广之术曰：先直广，即曰：下有若干步，以一为若干，以半为若干，以三分为若干，积分以尽所求分同之以为法，即耤直田二百四十步亦以一为若干，以为积步，除积步如法得从一步。不盈步者，以法命其分[4]。

《九章筭术》“积分”一词最先见之于少广章。少广术是：

少广术曰：置全步及分母子，以最下分母遍乘诸分子及全步，各以其母除其子，置之于左；命通分者，又以分母遍乘诸分子及已通者，皆通而同之，并之为法。置所求步数，以全步积分乘之为实。实如法而一，得从步。

“积分”就是分之积，“全步积分”是将1步化成分数后的积数。《九章筭术》、秦简《数》《筭书》、汉简《筭数书》少广术的例题的格式是：

今有田广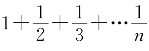。求田一亩，问：从几何？

其中《九章筭术》n=1，2，…12，秦简《数》n=1，2，…10，汉简《筭数书》n=1，2，…7。从即纵，今天常称之为长。此是以1亩作为“实”，即被除数，而以作为“法”，即除数。那么纵就是：

为了作除法，需要将通分。《九章筭术》的方法是：将自上而下排列，如左第1列，以最下分母n乘第1列各数，成为第2列，再以最下分母n-1乘第2列各数，成为第3列，如此继续下去，直到某列所有的数都成为整数为止，即

将右行即全部成为整数的这行所有的数相加，即

(n-1)(n-2)…×3×2+n(n-2)(n-3)…×3×2+…

+n(n-1)…×4×2+n(n-1)…×4×3+n(n-1)…×4×3×2

作为法。同时，右行最上的数n（n-1）…×4×3×2就是第1列每个数所扩大的倍数，也就是1步的积分。以1步之积分乘1亩即240步，作为实。实除以法，即得(www.xing528.com)

纵=1亩÷={240步×[n（n-1）×…4×3×2]}

÷{[(n-1)(n-2)…×3×2]+[n(n-2)(n-3)…×3×2]+…+

+[n(n-1)…×4×2]+[n(n-1)…×4×3]+[n(n-1)…×4×3×2]}。

这里没有使用常用的通分法，而是求出1步之积分。

《九章筭术》的积分就是将分数单位由分别是化 成公共的分数单位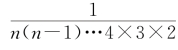的分母，n=1，2，…。1步就是由[n（n-1）×…4×3×2]个步积累而成。

在方程章麻麦问刘徽创造方程新术时刘徽总结说：

此麻麦与均输、少广之章重衰、积分皆为大事。

重申少广术的“积分”是重要问题。

《九章筭术》商功章委粟术刘徽注：

假令以三除周，得径。若不尽，通分内子，即为径之积分。令自乘，以高乘之，为三方锥之积分。

这段文字中有2个“积分”，前者的意义与《九章筭术》少广术的“积分”类似，都是长度的分之积。后者是关于体积的，下面再谈。