数学史自选集：天元式的表示法

作为设未知数列方程的方法，天元术含有两项必须的内容，一是立天元一为某某，相当于现今之设未知数某某为x。二是列出开方式，这就是根据问题的条件，先列出一个天元多项式，寄左；然后再列出一个与“寄左”者等价的天元多项式，作为“同数”；最后，两者如积相消，得到一个开方式，即现今之一元方程。

天元式的表示分幂次高低的排列和“元”或“太”的使用等方面。

前已指出，在最初，比如东平算经，天元术中的天元多项式用19个汉字表示常数项和未知数的各幂次，正次幂在上，负次幂在下。后来简化成以“太”即“太极”表示常数项，天元在上，地元在下，分别通过与天元、地元的相对位置表示未知数的正次幂和负次幂，称为古法。彦材法则颠倒了天元、地元的位置。李冶或其前的某人取消了地元，只用一个汉字“太”标出常数项，或用“元”（即天元）标出未知数的一次项，其他各项的幂次完全由其与“太”或“元”的相对位置决定。起初仍采取未知数的正幂在上，负幂在下的方式，这就是《河防通议》《测圆海镜》中使用的方法。后来李冶在《益古演段》中又借鉴彦材法，采取高次幂在下，低次幂在上的方式，遂成为13世纪下半叶、14世纪初的通用方式。其演变过程如下图所示。

比如《测圆海镜》卷三第5问[7]“草”中的天元式元表示多项式144x2+5 184x+2 488 320。《益古演段》第1问[13]中的天元式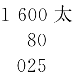表示多项式0.25x2+80x+1 600。

有时在天元式中不标出“元”字或“太”字。如《益古演段》卷中第39问[13]有一天元式是，表示多项式x2+228x+3 780。在《算学启蒙》中，几乎所有的天元式都不标出“太”或“元”字。如卷下“开方释锁门”第31问：

今有圆锥积三千七十二尺，只云：高为实，立方开之，得数不及下周六十一尺。问：下周及高各几何？

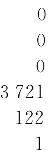术曰：立天元一为开立方数：，再自乘为高也：。再列开立方数，加不及，为下周也：。自之，又高乘之，为三十六段积：，寄左。列积，三十六乘之。与寄左相消，得开方式：，四乘方开之，得三尺，为开立方之数[14]。

前四个天元式都没有标出“太”或“元”，它们依次是x，x3，x+61，3 721x3+122x4+x5。

值得强调地是，天元式是指多项式或单项式，而不是指开方式[15]。许多数学史著述将开方式称为天元式，甚至称为“天元开方式”，说“‘天元开方式’就是一元高次方程”，说“现今代数学的一元高次方程a1xn+a2xn-1+…+an=0古代写为

这是不恰当的。“天元开方式”是作者因误解而杜撰的，李冶、朱世杰没有这种说法。一般说来，在天元术中，经过如积相消，得出的开方式不再标以“太”或“元”。如《测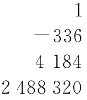圆海镜》卷三第5问之“草”[7]的开方式即表示成，它表示三次方程x3-336x2+4 184x+2 488 320=0。有的学者在引用这个开方式时在“4 184”后加了个“元”字[4]，当然不妥。

《益古演段》第6问[13]中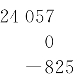，表示二次方程-8.25x2+24 057=0。

但是，《测圆海镜》中也有个别题目，在如积相消后得出的开方式中仍标以“元”，如卷三第2问[7]“法”之“草”中便有“相消得元，以平方开之”，其中的筹式亦表示方程-x2-80x+76 800=0。即使清刻本没有讹误，这也是极少数情形，而在《益古演段》及其之后，再没有这种表示，因此这不具有一般性。还有一种可能性，就是清刻本误加“元”字，在对天元式和开方式的表示方式认识不明确的情况下，这种讹误极易发生。正如20世纪许多作者在引用李冶、朱世杰的开方式时常在未知数的一次项旁加原书中没有的“元”字一样。无论如何，作为成熟的天元术而言，“如积相消”得出的开方式是不出现“元”字的，与天元式是有根本区别的。有人说“李冶的天元式，既可表示方程，又可表示多项式。从形式看，两者并无区别”[8]，当然是不妥当的。

参考文献

[1][元]祖颐.四元玉鉴后序.郭书春主编.中国科学技术典籍通汇·数学卷（1）[M].郑州：河南教育出版社，1993.

[2][元]李冶.敬斋古今黈[M].北京：中华书局，1990.

[3][清]阮元校.周易[M].十三经注疏[M].北京：中华书局影印，1980：46.

[4]梅荣照.李冶及其数学著作[J].钱宝琮等.宋元数学史论文集[A].北京：科学出版社，1966：104～148.

[5]郭书春.《河防通议·算法门》初探[J].自然科学史研究，1997，16（3）：223～232.李迪主编.第三届中国少数民族科技史国际学术讨论会论文集[C].昆明：云南科学技术出版社，1998：118～128.(www.xing528.com)

[6]李俨.测圆海镜研究历程考[J].学艺，1931～1932：11，12.中算史论丛：第四集.北京：科学出版社.1955：32～237.郭书春、刘钝等主编.李俨钱宝琮科学史全集（8）.沈阳：辽宁教育出版社.1998：37～222.

[7][元]李冶.测圆海镜.郭书春主编.中国科学技术典籍通汇·数学卷（1）[M].郑州：河南教育出版社，1993.

[8]孔国平.测圆海镜导读[M].武汉：湖北教育出版社，1996：8～10.

[9][元]李冶.测圆海镜自序.测圆海镜.郭书春主编.中国科学技术典籍通汇·数学卷（1）[M].郑州：河南教育出版社，1993.

[10][清]四库馆臣.测圆海镜提要[J].四库全书文津阁本[M].北京：商务印书馆，2006.

[11][清]刘岳云.测圆海镜通释[M].成都：尊经书局刻本，1896.

[12]郭书春主编.中国科学技术史·数学卷.北京：科学出版社，2010.

[13][元]李冶.益古演段.郭书春主编.中国科学技术典籍通汇·数学卷（1）[M].郑州：河南教育出版社，1993.

[14][元]朱世杰.算学启蒙.郭书春主编.中国科学技术典籍通汇·数学卷（1）[M].郑州：河南教育出版社，1993.

[15]郭书春.尊重原始文献 避免以讹传讹.自然科学史研究.2007，26（3）：438～448.

【注释】

[1]其中的算式，原文用算筹数字表示，为读者阅读方便计，这里改为阿拉伯数字，下同。

[2]原刻本误作大字，今根据前后体例改作小字。

[3]又倍东西并：原刻本讹作“又并东西行”，李锐校正。

[4]二之南北并，加入二之东西并：原刻本讹作“二之前泛数，加入四之东西并”，依李锐校正。

[5]“内带通勾分母”，清刻本作大字，依下文改作小字。

[6]“内带通积为母”，清刻本作大字，依上文改作小字。