洞渊的测圆问题及其天元术解决方法

《测圆海镜》卷十一第18题引用了洞渊测圆门的片段。许多学者认为，洞渊已能用天元术解决比较复杂的问题了。为了探讨这个问题，我们先看看这个题目：

或问：出北门一十五步，折而东行二百八步有树，出西门八步，折而南行四百九十五步见之。问荅同前。

法曰：先置南行步，内减一东二西并步，余二百七十一，为前泛率。次并一南二北，内减东行步，余三百一十七，为中泛率。次并东西步，以南行步乘之，于上位；又以西行乘南北，并得数，减上位，余一十万二千八百四十，为后泛率。乃以后泛率自乘，得一百五亿七千六百六万五千六百，为三乘方实。以前、中二泛相减，余四十六，以乘后泛数，为从。前、中二泛相乘，得八万五千九百〇七，加入二之后泛数，共得二十九万一千五百八十七，于上位；又倍东西并^[3]，以乘南北并，得二十二万三百二十，加上位，通得五十一万一千九百七为第一廉。二之南北并，加入二之东西并^[4]，得一千四百五十二，于上位；又以前、中二泛相减，余四十六，减上位，余一千四百六，为第二廉。一步常法，得半径。

草曰：立天元一为半城径，加入东行西行并，得元，为大勾也。又置天元，加入南行北行并，得元，为大股也。置西行八步，以大股乘之，得下式元。合以大勾除之。不除，寄为母，便以此为股尖也。置南行四百九十五步，减天元，得元。用分母大勾乘之。乘讫，得下式元。内减了股尖，余元，为小股也。内带大勾分母。置小股，合以大勾乘了，复以大股除之，为小勾。今为小股内已有大勾为母，更不须乘，只以小股元便为小勾也。内带大股为母。小勾小股相乘，得数为一个小勾股相乘直积，内带大勾股相乘直积为分母也。乃以半城径即天元也。除之，为一个弦较和也。此法本取勾外容圆，合以弦较和除二积，为勾外所容之圆。今用半天元圆径除一个积，则却得一个弦较和也。内依旧带大积分母也。寄左。然后再置小股元，合用大积乘之，缘内已带大勾分母。今只用大股元乘之，得，为大积所乘小股，于上。再置小勾，合用大积乘之，缘内已带大股分母，合只用大勾元乘之，得元，为大积所乘之小勾也。以此小勾减上小股，得，即带分小较也。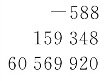又二因小较，得此下式元为带分二较也。又以大勾股直积乘二之天元半圆经，得，为一个带分弦较较也。弦较较乘弦较和为二直积。既以圆径除二直积为弦较和，则是圆径为弦较较也。今又为半天元圆径除一积为弦较和，故倍天元半径作一个弦较较也。遂将此弦较较加入前二较，得元，亦为一个弦较和也。与寄左相消，得下式：。开三乘方，得一百二十步，即半城径也，合问。

又法：此问系是《洞渊》测圆门第一十三，前答亦依洞渊细草，用勾外容圆术，以如于弦较和。然其数烦碎宛转费力。今别草一法，其廉、从与前不殊，而中间段络径捷明白。方之前术，极为省易，学者当自知也。立天元为半径，副之。上并加东西行，得元，为通勾率。下并加南北行，得元，为通股率，乃置西行八步，以通股乘之，得下元。合通勾除，不除，寄为母，便以此为南小股也。又置南行四百九十五步，内减天元，得元。用通勾乘之，得元。内减了南小股，余下式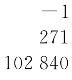元，为股圆差也。内带通勾分母。^[5]又置北行一十五步，以通勾乘之，得元。合通股除，不除，寄为母，便以此为北小勾也。又置东行二百八步，内减天元，得元。用通股乘之，得元。内减了北小勾，余元，为勾圆差也。内带通股分母。乃以二差相乘，得下式元，为半段圆径幂也。内带通积为母^[6]，寄左。然后以通勾通股相乘，得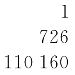元。以天元幂乘之，得。又倍之，得下式：，为同数。与左相消，所得廉、从一与前同。合问。[7]

这是求圆城半径，设为x。如图，已知出西门a‴=8，出北门b″=15，折而东行a2+a″=208，折而南行b1+b‴=495，则

接着，由勾外容圆公式，得到同等于c7+b7-a7的两个天元式(www.xing528.com)

将上2式如积相消，得x3-542x2-132 239x+55 739 280+=2x3+864x2+379 668x+60 469 920。整理成

-x4-1 406x3-511 907x2-4 730 640x+10 576 065 600=0

洞渊测圆图

清中叶四库馆臣首先注意到这个问题中提到洞渊测圆门，并说李冶“于此问又明其为洞渊测圆门第十三题”[10]。清末刘岳云《算学丛话》进而发现《测圆海镜》卷十一第17、18二问属于同类，他说：“依《海镜》理，出西门北门不得有行步，而卷十一后二问（按：即第17、18问），出北门行十五步，出西门行八步。详书意，盖于本勾股形外展大其勾股，勾为三百四十三，股为六百二十三，其八与十五即距城之数，为小勾股率。书中引为洞渊测圆门第十三题，然则洞渊之书，以圆内圆外互求，而九容乃其一端耳。”[11]李俨则认为：“李冶《测圆海镜》卷十一后二问和全书体例不同，疑并出于洞渊。”他将此二问的有关部分归于“洞渊的测圆术”。但是认为第18问的“又法”主要指下面的草，“为李冶所作”[6]。后来学术界基本上沿袭李俨的说法。但有的学者引用第18问时，却有意无意不引“又法”二字[8]，给读者造成紧接“又法”的“此”自然是指“又法”前面的全部内容，即不仅“法”，而且“草”也是洞渊所作的错觉。

此问是洞渊测圆门第13问是没有疑问的。问题在于，洞渊的“此问”含有哪些内容？我们认为，这里的“此问”含有题设、答案和“法”三种内容，不应该含有“草”。我们知道，自《海岛算经》起，一直到北宋的《益古集》《议古根源》等数学原著，都有“术”或“法”，而没有“细草”。为之作“细草”的是后人。没有证据显示洞渊测圆门与其他著作不同。因此，此问中的“法”自然是洞渊的，李冶指出其关键是“用勾外容圆术，以如于弦较和”。而“草”则不然。李冶说的“亦依洞渊细草”不是说这是洞渊的“细草”，而是说李冶依洞渊的“法”作的“细草”。将“法”之后的“草”说成是洞渊的，根据似不足。“又法”及其“草”自然是李冶所撰，李俨的看法是对的。其中应该表述的“实”“第一廉”“第二廉”“常法”等则在下面的“草”展现，“又法”中没有赘述。

总之，从李冶的文字中看不出石信道与洞渊通晓天元术[12]。