《九章算术》的抽象化方法及其应用

《九章算术》的术文即公式、解法大都具有普适性和一定程度的抽象性，尤其是前五章及盈不足章的解法都是相当抽象的纯数学公式、解法，然而也有一些术文未离开其题设的具体对象，甚至具体数值。刘徽是按—般性证明这些公式、解法的，然未改写《九章算术》的术文。贾宪则提出抽象性术文，尤以方程术和勾股问题诸术最为典型。

方程术即线性方程组解法是《九章算术》最杰出的成就，它实际上具有普适性，然其术文借助禾实来阐述，正如刘徽所说：“此都术也。恐空言难晓，故特系之禾以决之。”[5]刘徽以齐同术论证方程术，并创造了互乘相消法。贾宪则提出了不依赖于具体对象的术文：

术曰：本倍折减损之问，初无活法，今述此意。排列逐项问数，某物某物共直几钱为一行，某物某物共直几钱为一行。命首位物多者为主，彼七此五，以七为多。以邻行数增乘求等。数等可以减损。余物与价即总数也。亦例乘之，物既增，余物与价亦各升为一体。以原多物行内数目。对减，谓物减物，钱减钱，求轻一位。其余次第增减，增少数与多数为停，如求对除以求位简。价可为实，物可为法而止。法实皆一位也。以法除之。商除。[8]

这条术文虽未脱离开物与钱，然不再系之以禾，且行数不限，其抽象性比《九章算术》进了一大步。贾宪提出以物多者为主，亦可减省运算。

对勾股问题，贾宪首先提出了“句股生变十三名图”。他说：“句股弦并而为和，减而为较，等而为变、为段，自乘为积、为幂。”[8]十三名即勾（a）、股（b）、弦（c）、勾股较（b-a）、勾弦较（c-a）、股弦较（c-b）、勾股和（a+b）、勾弦和（a+c）、股弦和（b+c）、弦较和[c+（b-a）]、弦和和[（a+b）+c]、弦和较[（a+b）-c]、弦较较[c-（ba）]十三种关系，贾宪还指出了这些关系变成勾股较、股弦较、弦和较的段数。我们知道《九章算术》只出现了a，b，c及c±a，c±b，b-a，（a+b）+c九种关系，刘徽注又补充了a+b，（a+b）-c两种，对c±（b-a）则未涉及，都不完备。而贾宪的十三名图实际上包含了勾、股、弦及其和、差的全部可能的关系。贾宪说这些关系“有用而取，无用不取，立图而验之”，表明“句股生变十三名图”对他的勾股理论有提纲挈领的作用。

接着，贾宪把勾股章所有系之于具体对象或数值的术文抽象成纯数学方法。比如对“户高多于广”这类已知弦与勾股差求勾、股的问题，《九章算术》的术文是：

术曰：令一丈自乘为实，半相多，令自乘，倍之，减实，半其余，以开方除之。所得减相多之半即户广，加相多之半即户高。[5]

以一丈、相多、户广、高立术。贾宪的方法是：

句股较与弦求股法曰：弦自乘，半较自乘，倍之，减积，余，半之，开方得半和。^[2]减半较，为句；加较为股^[3]。[8]

贾宪的方法则以弦、（勾股）较、和立论。

又如，《九章算术》甲乙同立问的术文含有勾股数公式，是重大成就，然而却以数字立术：

术曰：令七自乘，三亦自乘，并而半之，以为甲邪行率。邪行率减于七自乘，余为南行率，以三乘七为乙东行率。置南行十步，以甲邪行率乘之，副置十步，以乙东行率乘之，各自为实，实如南行率而一，各得行数。[5]

刘徽的证明舍弃了具体数字，然未改写术文。贾宪则将其抽象成仅依赖于勾弦和率、股率的方法：

法曰：句弦和自乘，股率自乘，并而半之，为弦。以减和求句。股率乘句弦和率求股。以所有句数乘所求句、股、弦三率，为列实，以所有句率为法除之。[8]

这就是勾股数公式：a∶b∶c=（m2-n2）∶mn∶（m2+n2）。(www.xing528.com)

《九章算术》“勾股容方”问的术文是抽象性的。贾宪又提出了“勾股旁要法”。这是自二郑注“九数”之后现存数学著作中第一次出现“旁要”的名称，值得重视。

句股旁要法曰：直田斜解句股二段，其一容直，其一容方，二积相等。余句余股相乘亦得容积之数。句股相乘为实，并句股为法，除之，得句中容方。积内有一容直，故用句除横积并股除直积，得所容方也。以容直或方外余句股相乘得容积之实。句股中直积一段，大句股一段，小句股一段。如余句而一，得股长。如余股而一，得句阔^[4]。[8]

贾宪方法的前半段是《九章算术》术文的改写。注中提出了一个重要原理。一长方形分成二勾股形，则从弦上一点出发的容方容直面积相等。（实际上，从公共弦上任一点作两条分别平行于两边的垂线，则所容两长方形面积相等。）横积是容方右侧的长方形，其面积为方×余勾，直积是容方上面的长方形，其面积是方×余股。因此，贾宪又提出一公式：方=。

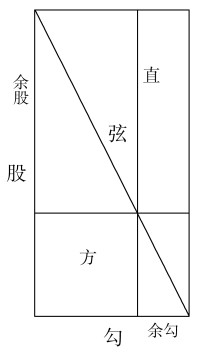
图1

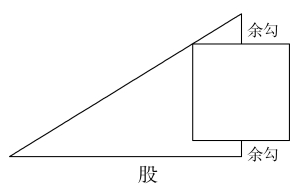
图2

及

这里考虑勾股容方与容直、横积、直积及与勾、股的互相关系，都是从旁取要，很可能是“旁要”的本义。贾宪这一方法可能提供了解决千余年未得其解的“旁要”之谜的钥匙。

对测望问题，贾宪也将《九章算术》术文改写成纯数学方法。如“出南北门测邑方”问，《九章算术》的方法是：

术曰：以出北门步数乘西行步数，倍之为实，并出南门步数为从法，开方除之即邑方。[5]

贾宪的方法是：

术曰：余句乘股，倍之为实，并二余句为从，开方除之。[8]