郭书春数学史自选集下册中针对原文错误的校勘纠正

原文确有错误而戴震等人校改亦有不恰当的情形。南宋本、大典本等目前最古的传本的舛误文字，后人对之作出的校勘，如无其他版本依据，或不是通过本校法、他校法得到的，而是通过理校法得到的结论，只是合理的推论，而不能成为定论。本文第一部分中笔者对前人的漏校之处提出的校勘意见当然也是如此。既然是合理推论，当然有仁智各见的情形。不过根据算经本身的结构、体例、算理及衍脱规律等，可以肯定某些校勘是错误的。试举几例，《九章算术》卷九“户高多于广”问刘徽注第二段，在通过出入相补原理证明了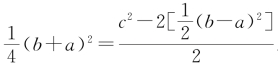之后的文字，大典本、杨辉本都是“其于大方弃四分之一”。显然有讹舛。戴震改为“其于大方弃四分之三，适得四分之一”，钱校本认为戴校似无必要，仅改“弃”作“得”，汇校本从。校证本认为“一”系“三”之误。笔者现在认为“弃”系“者”之误。“二人同所立”问刘徽注中大典本、杨辉本有“术以可使为分母”显然不通。戴震改作“术以勾弦并为分母，差为分子”，李潢本、钱校本删戴校之“差为分子”，钱校本又于“并”下补“率”字，汇校本从。笔者现在认为，此句当为“术以同使无分母”，“可”与“同”，“爲”与“無”皆形似而误。这里的“同”就是上文“通而约之”所产生的“同”，即“勾弦并率”。《海岛算经》第六问李淳风等注释中戴震辑录本有“以步里法除之”，亦不通。校证本改“步里法”作“寸里法”，不妥，正如上述，应为“里寸法”。

总的来说，尽管汇校本《九章算术》已经纠正了戴震等人520余条校勘错误，目前需要继续纠正的错校仍然远远超过需要校勘的漏校之处。因此，纠正前人的错校，仍然是《算经十书》校勘中的主要任务。

参考文献

[1]宋刻算经六种.北京：文物出版社影印，1980.下称南宋本.

[2]汲古阁主人毛扆影抄南宋本诸算经.北平故宫博物院影印.天禄琳琅丛书，1932.下称汲古阁本.

[3]《永乐大典·筭》（1408）.现存卷16343、16344.北京：中华书局影印，1960.下称大典本.*郭书春主编.中国科学技术典籍通汇·数学卷（1）影印.郑州：河南教育出版社，1993.

[4]周髀筭经.明胡震亨刻本.上海古籍出版社影印，1990.下称明刻本.

[5][清]武英殿聚珍版丛书所收《周髀算经》《九章算术》等七部算经.下称聚珍版.郭书春主编.中国科学技术典籍通汇·数学卷（1）影印.郑州：河南教育出版社，1993.

[6][清]《四库全书》所收《周髀算经》《九章算术》等七部算经.下称四库本.台北：商务印书馆影印其文渊阁本，1983.*北京：商务印书馆影印其文津阁本，2006.

[7]戴震校.算经十书.孔继涵刻微波榭本.1777年或其后.

[8]钱宝琮校点.算经十书.北京：中华书局，1963.郭书春、刘钝等主编.李俨钱宝琮科学史全集（4）.沈阳：辽宁教育出版社，1998.

[9]郭书春.《九章筭术》版本卮言.第二届科学史研讨会（台北，1989）汇刊.1991.*郭书春汇校.九章筭术新校·附录三.合肥：中国科学技术大学出版社，2014.

[10]江晓原.译注周髀算经.中国古代科技名著译丛.沈阳：辽宁教育出版社，1996.(www.xing528.com)

[11][宋]李诫.营造法式.四库全书文渊阁本.台北：商务印书馆，1986.

[12]李潢.九章算术细草图说引.郭书春主编.中国科学技术典籍通汇·数学卷（4）影印.郑州：河南教育出版社，1993.

[13]李继闵.九章算术校证.西安：陕西科学技术出版社，1993.下称校证本.

[14]郭书春汇校.汇校九章算术.沈阳：辽宁教育出版社，1990.*郭书春汇校.九章筭术新校.合肥：中国科学技术大学出版社，2014.

[15]郭书春.再论《九章筭术》的校勘.汉学研究（台北）.1998，16（1）.*郭书春汇校.九章筭术新校·附录三.合肥：中国科学技术大学出版社，2014.

[16]荀子集释.王先谦集.北京：中华书局，1988.

[17]商子.百子全书.杭州：浙江人民出版社，1984.

[18]白尚恕.九章算术注释.北京：科学出版社，1983.

[19][清]李潢.缉古算经考注.郭书春主编.中国科学技术典籍通汇·数学卷（4）影印.郑州：河南教育出版社，1993.

【注释】

[1]*此说不妥，四库文津阁本《九章算术》在戴震在世时已抄录。