近年发现的战国秦汉数学简牍

自1983年底1984年初湖北荆州张家山247号汉墓发现约200支数学竹简《筭数书》之后，近20年间，在出土数学简牍方面没有什么新的重大收获。而近10年来，则不断有发现数量不等的战国秦汉数学简牍的消息传来，令中国数学史界十分振奋。这几批数学简牍有的基本整理完毕，已经出版，有的正在整理，谨根据已经发布的消息，以这些数学简牍产生的年代为序，介绍如下：

清华大学收藏的战国算表 清华大学出土文献研究与保护中心收藏的战国《算表》为一表格形式的竹质册书，由21枚竹简组成，距今约2300年。全表凡441个单元格。纵向19行，横向19列，右栏与上栏分别由下至上，由左至右依次书写，基数1至9及十位数10至90诸数。它们的乘积分别记入纵横栏的交叉处。因此其核心为九九表，其他皆为核心部分之扩展与延伸[1]。

湖南里耶出土秦九九表木牍 2002年湖南湘西里耶古井中出土了秦九九表木牍（图1）[2]，凡113字。20世纪以来出土过许多有关九九表的竹简，但都是片断，以里耶秦九九表最为完整。

岳麓书院收藏的秦简《数》 湖南大学岳麓书院于2007年12月在香港古董市场收购了一批竹简，经专家组鉴定为秦简。我们最感兴趣的当然是其中的《数》（图2）。目前经过整理的《数》共有236枚编号简，18枚残片（无编号）。保存较为完好的简长度在27.5厘米左右，宽度约为0.5～0.6厘米。简有上、中、下三道编绳。0956号简的背面写有一“数”字，是为书名。[3]现已整理完毕并出版了《岳麓书院藏秦简（贰）》。[4]《数》的完整算题一般包括条件、问题、答案、术文四部分，少数算题有题名。单独成文的“术”19例，例如合分术、乘法口诀等。记录谷物体积重量比率、兑换比率的简34枚，记录衡制的简3枚。秦简《数》的内容包括分数四则运算、田地面积、农作物产量、谷物的比重及兑换率、衰分、少广、体积、盈不足、勾股及营军、租误券等。[5]这些类型的问题在《筭数书》中差不多都有，唯有“圆材薶（埋）地”问在现在已经整理的其他简牍中没有见过。这实际上是一个勾股问题：

有圆材薶地，不智小大，斲之，入材一寸而得平一尺，问材周大几可。即曰，半平得五寸，令相乘也，以深一寸为法，如法得一寸，有以深益之，即材径也。

它与《九章筭术》勾股章勾股锯圆材问基本一致而文字古朴。[6]《九章筭术》的这个问题是：

今有圆材埋在壁中，不知大小。以锯锯之，深一寸，锯道长一尺。问：径几何？

荅曰：材径二尺六寸。

术曰：半锯道自乘，如深寸而一，以深寸增之，即材径。[7]

刘徽将锯道一尺视为勾，圆材直径视为弦，而将锯深一寸视为股弦差之半。那么《九章筭术》实际上应用了公式

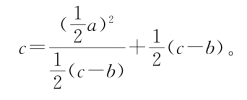
图1　湖南里耶出土的秦九九表木牍

图2　秦简《数》的部分简（岳麓书院供图）

北京大学收藏的秦数学简 2010年初，香港友人捐赠一批秦简给北京大学。其中与数学相关的内容所占比重最大，有卷三、四、七、八凡四卷，总计竹简有400余枚。[8]此外还有“九九术”木牍一方。另外，简牍中混杂的三组竹制算筹与数学也有密切关系，应该是主人生前用来计算和占卜的工具。北大藏秦数学简牍的内容采取以类相从的方式，即将同类的问题归于一组。其数学方法与题目的结构有二种形式：一种是先以“某某述（术）曰”的形式叙述计算方法，然后列出多道例题，这些例题只有数据的差别；一种是先举例题，然后以“某某述（术）曰”的形式概括计算方法。大家知道，这是《九章筭术》中两种最主要的体例。

卷三共82枚以及卷四的一部分，主要内容是各种数学计算方法和例题的汇编，与张家山汉简《筭数书》、岳麓秦简《数》及《九章筭术》相似。由于未发现篇题，整理者根据内容先将其定名为《算数书》，我建议改为《算书》或《数书》，整理者取前者。卷四是多种古书的杂抄。其中的《算书》分为甲、乙两篇。卷七和卷八的形式整齐划一，每简内容仅有数字的差别，而且未出现任何具体的地名、人名，显然不是当时丈量田亩、征收租税的档案记录，而应该是供人学习田亩、租税计算的一种特殊算术教材或参考书。在卷八一枚简的背面近上端处写有“田书”的篇题，应是这类书的专名。这两卷简册涉及的数学运算比较简单，但是对研究战国晚期至秦代的土地、赋税制度很有帮助。

《算书》甲篇可分为四个部分：

第一部分有32枚简，800余字，内容是以鲁久次和陈起二人问对的形式，通过陈起的回答，详尽论述了古代数学的起源、作用和意义[9][10]。原无篇题，拈篇首语定名为《鲁久次问数》^[1]。(www.xing528.com)

鲁久次问数于陈起曰：“久次读语、计数弗能并勶，欲勶一物，可物为急？”陈起对之曰：“子为弗能并勶，舍语而勶数，数可语殹，语不可数殹。”

“鲁久次”“陈起”二人，史籍未载。陈起应是一位“数学家”，鲁久次从其问数。《周髀筭经》载有陈子答荣方问。陈起是否就是陈子，不得而知。勶即“彻”，通晓，西汉中期以后多避汉武帝讳改为“通”。鲁久次问陈起：在读语和计数不能兼通的情况下，想要先通晓一种，哪一种更急迫？陈起回答：如果不能兼通，应该舍弃“语”而先通“数”，因为“数”可以兼盖“语”的功能，“语”却没有“数”的作用。此处将“语”“数”并举，颇能反映当时人的知识结构。战国时期举凡诸子百家、历史掌故皆称“语”。陈起贬低“语”而抬高“数”，这种“重理轻文”的倾向在战国诸子中极为罕见。

随后陈起提出“天下之物，无不用数者”，详细列举在测天量地、音律以及社会管理和生产生活中的种种应用，指出“民若不知度数，无以知百事经纪”。这样论述数学对于宇宙万物和人类社会的作用和意义，足可以与《孙子筭经·序》相媲美。

在本篇的结尾，陈起有一段非常重要的话：

故夫古圣贤书竹白[帛]以教后世子孙，学者必慎毋忘数。凡数之保[宝]莫急郦首，隶首者筭之始也，少广者筭之市也，所求者毋不有也。

“郦首”即传说中的黄帝之臣“隶首”，《史记·历书》司马贞《索隐》引《系本》（即《世本》）及《律历志》曰：“黄帝使……隶首作算数”[11]，后世文献关于“隶首作数”的记载盖皆本之《世本》。这一古史传说现在得到了出土资料的印证，“郦（隶）首者筭之始”就是说隶首是算术的始祖。“少广”是《九章筭术》、张家山汉简《筭数书》、岳麓秦简《数》中的一种数学方法。“少广者筭之市”^[2]，是说“少广”术就像一个市场，学习算术者所需要的东西都可以在其中找到，即“所求者毋不有也”。值得注意的是，《算书》甲篇的第三部分“算题汇编”的第一题即为“少广”。

《算书》甲篇的第二部分是“九九术”，共8枚简，分上下五栏抄写，始于“九九八十一”，终于“一一而一”，与湖南里耶出土的九九表木牍基本相同，仅行款略有差异。可见“九九术”所采用的表格形式至迟在战国晚期已经定型，此后流传过程中很少发生变化。

第三部分“算题汇编”是《算书》甲篇的主体。其基本单位（学者多称为“算题”）的结构主要分为以下三类：

（1）先以“某某述（术）曰”或“曰某某述（术）”开头叙述计算方法，如果有多种算法，则用“其一述（术）曰”的形式补充在后。然后列举例题，例题往往有多道，每道题只有具体数据的差别。

（2）先举例题，然后用“其述（术）曰”的形式概括计算方法，张家山汉简《筭数书》和《九章筭术》中的算题大多属于这种结构。

（3）仅叙述计算方法而无例题，为数不多，主要见于抽象运算，如“乘分”“合分”“约分”等。岳麓秦简《数》中的“乘分”算题还附带抄录了乘法口诀[4]，北大秦简的“乘分”则无乘法口诀，这一点与张家山汉简《筭数书》相同。

若干同类的内容编为一组，有一枚单独的“标题简”置于本组之前。“标题”书于该简正面上端，其上将竹简头端涂成黑方块，作为提示符号。可确定的这类“标题”有“田”“租禾”“租枲”“自为实”等，概括了本组算题的内容。从算题的分组和“标题”的设置看来，主要是针对日常生产生活中遇到的各种实际问题来分类（比如租税计算除“租禾”外还有“租枲”），而不是以同类数学方法的总结和归纳为原则，体现了早期数学文献较为原始的特征。这种同类算题的分组与《九章筭术》、岳麓秦简《数》相类似的“组群”性特点，但《数》未发现北大秦简这样的“标题简”。

《算书》甲篇的第四部分是衡制换算，包括石、钧、斤、两、甾（锱）、朱（铢）等单位的相互换算，如“一石而四钧”“一钧而卅斤”等，其中一部分抄写于《日廷》下部的空白处。岳麓秦简《数》也有类似的内容。

《算书》乙篇由多道并列的算题组成，每道算题内部也分为算法和例题，但算题之间看不出甲篇那种“以类相从”的分组。算题内容包括金、布、锡、钱的交易比率，土方及粮食体积计算，距离计算等。每道算题都有自己的题名。

湖北博物馆藏的睡虎地汉数学简 湖北睡虎地汉墓出土了216枚数学竹简，定名为《算术》。竹简略有残缺，文字完整，字迹清晰。同时出土的最后一个历日是汉文帝后元七年（即公元前157年），有10枚简的照片发在《江汉考古》上。这批竹简正在整理，据初步了解，有一些题目与秦简《数》、汉简《筭数书》《九章筭术》相似，但是也有这些著作乃至整个中国传统数学著作中没有的内容^[3]。

此外安徽阜阳及山东临沂银雀山也有数学简牍的片断出土。阜阳汉简中有《九章筭术》均输术的残存文字。^[4]

值得注意的是：《九章筭术》各种不同的体例[12]在岳麓秦简《数》、北大秦简《算书》都存在，而且以术文统率例题的形式占的比重最大，可见这是秦与先秦数学的共同特点，反映了先秦比较重视数学理论研究。