斩都与刍甍：形状、体积公式及争议探讨

“斩都”条云：

斩都^[1]斩都下厚四尺，上厚二尺，高五尺，袤二丈，积百卅三尺少半尺。术曰：倍上厚，以下厚增之，以高及袤乘之，六成一。

设上、下厚分别为a1，a2，袤为b，高为h，则“斩都”的体积公式为

将题目的数值代入上述公式，便得到“斩都”体积

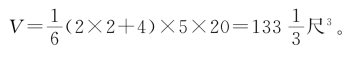
公式（1）与人们熟悉的《九章筭术》中的“刍甍”的求积公式十分相似。《九章筭术》云：

术曰：倍下袤，上袤从之，以广乘之，又以高乘之，六而一。[4]

刍甍的形状如图1所示。设它的上、下袤为a1，a2，广为b，高为h，则其体积公式是：(www.xing528.com)

图1　刍甍

图2　斩都

（1）（2）两式形式上相似，笔者据此曾经认为“斩都”就是《九章筭术》的刍甍。但是在“斩都”的公式（1）中是“倍上厚”即2a1，而“刍甍”的公式（2）中是“倍下袤”即2a2，两者形状不可能相同。2006年8月在洪万生教授在台北召集的“《筭数书》及相关简牍国际研讨会”上，学者们就“斩都”的形状展开了热烈讨论，但莫衷一是。其中一种意见是“斩都”为图2的形状，笔者认为较有道理。近日顷接清华大学（台湾新竹）陈良佐教授寄来大作《〈筭数书〉中体积问题与中国古代体积理论的四个基本原理》，发现其中也将斩都绘成图2的形状。

斩都的体积公式（1）是正确的，那么它是怎么得到的呢？这个公式相当复杂，显然不可能由直观、悟性得到，当时必有某种推导。我们认为，公式（1）是由棊验法得到的。