郭书春数学史自选集：由积求广，从与少广术

《筭数书》中尽管没有《九章筭术》的“方田术”，却有“方田术”的逆运算，还有“大广术”的逆运算。这就是已知“方田”即长方形的面积及“从”或“广”，求其“广”或“从”。这里包括求广、求从和少广3种情形；实际上，少广术也是求从的方法，只不过更复杂一些。

1.由积求广

由积求广，《筭数书》称为“启广”，是其第65条：

启广 田从卅步，为启广几何而为田一亩？曰：启八步。术曰：以卅步为法，以二百四十步为实。启从亦如此。

这是一个非常简单的问题：

广=240（平方）步÷30步=8步。

运算中没有分数，应该是“方田术”的逆运算。

2.由积求从

不言而喻，《筭数书》将由积求从称为“启从”，是其第66条：

启从 广廿三步，为启从求田四亩。曰：启从四十一步二十三分步之十七。术曰：直四亩步数，令如广步数，而得从一步。不盈步者，以广命分。复之，令相乘也。有分步者，以广乘分子，如广步数，得一步。广八分步之六，求田七分步之四，其从廿一分之十六。广七分步之三，求田四分步之二，其从一步六分步之一。求从术：广分子乘积分母为法，积分子乘广分母为实，实如法一步。即以广、从相乘，凡令分母相乘为法，分子相乘为实，实如法一。

此条有2段抽象性术文。前者的面积与广都是整数，求从：

从=面积÷广。

还提出，如除不尽，便以广命名一个分数。此术只有一个例题：已知广23步，面积为4亩=240（平方）步×4=960（平方）步，那么，

从=960（平方）步÷23步=41步。

第2段术文是处理面积与广有分数的情形，包括两者都是分数的问题，比《筭数书》的“径分术”除数都是整数要广泛、抽象，与《九章筭术》的“经分术”的内容一致。

值得注意的是，术文提出“广分子乘积分母为法，积分子乘广分母为实”，亦即

这就是颠倒相乘法。笔者过去认为，颠倒相乘法是刘徽提出的[7]，显然是错误的。此术有2个例题，积与广都是分数。第1题是：已知广6/8步，面积4/7（平方）步，

3.少广术(www.xing528.com)

《筭数书》第67、68条是少广问题。前者是“少广术”，后者是“少广术”的例题。“少广术”是：

少广 求少广之术曰：先直广，即曰：下有若干步，以一为若干，以半为若干，以三分为若干，积分以尽所求分同之，以为法。即耤直田二百四十步，亦以一为若干，以为积步。除积步如法，得从一步。不盈步者，以法命其分。有曰：复之，即以广乘从，令复为二百四十步田一亩。其从有不分者，直如法增不分，复乘之，以为小十^[5]；有分步者，以广乘分子，如广步数，得一步。

此条有2段抽象性术文，前者是“少广术”，与《九章筭术》少广章的“少广术”程序一致而文字有所不同。应该说，这里的程序更抽象一些，文字更古朴一些。

第68条是少广术的9个例题：

少广 广一步、半步。以一为二，半为一，同之三，以为法。即值二百四十步，亦以一为二。除如法，得从一步，为从百六十步。因以一步、半步乘。下有三分，以一为六，半为三，三分为二，同之十一。得从百卅步有十一分步之十。乘之田一亩。下有四分，以一为十二，半为六，三分为四，四分为三，同之廿五。得从百一十五步有廿五分步之五。乘之田一亩。下有五分，以一为六十，半为卅，三分为廿，四分为十五，五分为十二，同之百卅七。得从百五步有百卅七分步之十五。乘之田一亩。下有六分，以一为六十，半为卅，三分为廿，四分为十五，五分为十二，六分为十，同之百四十七。得从九十七步有百四十七分步百四十一，乘之田一亩。下有七分，以一为四百廿，半为二百一十，三分为百四十，四分为百五，五分为八十四，六分为七十，七分为六十，同之千八十九。得从九十二步有千八十九分步之六百一十二。乘之田一亩。下有八分，以一为八百四十，半为四百廿，三分为二百八十，四分为二百一十，五分为百六十八，六分为百四十，七分为百廿，八分为百五，同之二千二百八十三，以为法。得从八十八步有二千二百八十三分步之六百九十六。乘之田一亩。下有九分，以一为二千五百廿，半为千二百六十，三分为八百四十，四分为六百卅，五分为五百四，六分为四百廿，七分为三百六十，八分为三百一十五，九分为二百八十，同之七千一百廿九，以为法。得从八十四步有七千一百廿九分步之五千九百六十四。乘之成田一亩。下有十分，以一为二千五百廿，半为千二百六十，三分为八百四十，四分为六卅，五分为五百四，六分为四百廿，七分为三百六十，八分为三百一十五，九分为二百八十，十分为二百五十二，同之七千三百八十一，以为法。得从八十一步有七千三百八十一分步之六千九百卅九。乘之成田一亩。

与《九章筭术》“少广术”的例题一样，这些题目实际上都是：

田广=，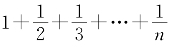

求田1亩，问从几何？只不过《筭数书》中n=10，而《九章筭术》中n=12，相差2个更复杂的题目。我们以n=6为例。《筭数书》的解法是：

广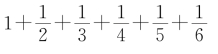

法 60+30+20+15+12+10=147

从=240（平方）步×60÷147步=97步。

这里以1为60。显然，60是2，3，4，5，6的最小公倍数。而《九章筭术》的解法是：

广

法 120+60+40+30+24+20=294

从=240（平方）步×120÷294步=97步。

以1为120。120不是2，3，4，5，6的最小公倍数，而是它们的乘积。不知为什么张苍、耿寿昌在整理《九章筭术》时没有使用最小公倍数60，而使用烦琐的120。不过起码可以说明，张苍等对通分中使用最小公倍数的优越性没有认识。然而，《筭数书》的答案不是最简分数，《九章筭术》则化成了最简分数。