1.粟米互换
粟米互换是中国传统数学的重要内容，用比例方法即今天所谓“三率法”解决。它在《九章筭术》中称为“今有术”，当时是专门用于解决粟米互换问题的。《筭数书》也有几个粟米互换问题，都用比例算法求解。但是，《筭数书》未提出抽象的今有术。
（1）粟米之法 “粟米之法”是《九章筭术》在粟米章卷首列出的各种粟米的互换比率表。《筭数书》没有“粟米之法”之名，然而，在第35条“程禾”，第39条“粺毇”，第41条“粟为米”等条中专门给出了某些粟米的互换比率。“程禾”条是：
程禾 程曰：禾黍一石为粟十六斗泰半斗，舂之为粝米一石，粝米一石为糳米九斗，糳米九斗为毇米八斗。程曰：稻禾一石为粟廿斗，舂之为米十斗，为毇、粲米六斗泰半斗。麦十斗为
三斗。程曰：麦、菽、荅、麻十五斗为一石，禀毇、糳者，以十斗为一石。
“程”是标准，“程禾”就是官方规定的某些粟米互换的标准。这里共有3项。第1项中各粟类的互换标准是：
禾黍10 粟16
粝米10 糳米9 毇米8
化成整数，便是：
禾黍30 粟50 粝米30 糳米27 毇米24
与《九章筭术》“粟米之法”比较，禾黍为“粟米之法”所没有，“程禾”中的毇米率等于“粟米之法”的糳米率，“程禾”中的糳米率等于“粟米之法”的粺米率，而两者的粟和粝米率分别相同。
第2项中各粟类的互换标准是：
稻禾10 粟20 米10 毇米6
麦10 
3
化成整数：
稻禾30 粟60 米30 毇米20 麦30 
9
除了“米”（一般指粝米）与第1项及“粟米之法”完全相同外，其他各种都与之不同，甚至完全不同。这说明这一项产生的时代不仅与《九章筭术》“粟米之法”不同，也与同书同一条的第1项不同。
第3项说米类10斗为1石，麦等谷类15斗为1石，与《九章筭术》商功章“程粟”中“其米一斛积一尺六寸五分寸之一，其菽、荅、麻、麦一斛皆二尺四寸十分寸之三”完全一致。
“粺毇”条是：
粺毇 米少半升为粺十分升之三，九之，十而一。米少半升为毇米十五分升之四，八之，十而一。米少半升为麦半升，三之，二而一。麦少半升为粟廿七分升之十，九母，十子；十之，九而一。麦少半升为米九分升之二，参母，再子；二之，三而一。麦少半升为粺五分升之一，十五母，九子；九之，十五而一。麦少半升为毇四十五分升之八，十五母，八子。粺米四分升之一为粟五十四分升之廿五，廿七母，五十子。粺米四分升之一为米十八分升之五，九母，十子。粺米四分升之一为毇米九分升之二，九母，八子。粺米四分升之一为麦十二分升之五，九母，十五子。毇米四分升之一为米十六分升之五，八母，十子。毇四分升之一为粺卅二分升九，八母，九子。毇米四分升之一为麦卅二分升之十五，八母，十五子。毇米四分升之一为粟四十八分升之廿五，廿四母，五十子。
这个粟米互换表很长，实际上只涉及到5种粟米，其比率如下：
粟50 米30 粺米27 毇米24 麦45
其中毇米率与“粟米之法”的糳米率相同。
“粟为米”条是：
粟为米 麻、麦、菽、荅三而当米二，九而当粟十。粟五为米三。米十为粺九，为毇八。麦三而当稻粟四。禾粟五为稻粟四。
这一条很简洁，涉及的粟类却最多，它们是：
显然，它完全涵盖了第39条的内容，其率也相同。同时，前4种的率与《九章筭术》“粟米之法”完全相同，毇、稻粟、禾粟的率分别与“粟米之法”的糳米、稻、粝饭相同。此外，“程禾”与“粺毇”“粟为米”条中的毇米，都是“粟米之法”中的糳米。
（2）粟米互换 《筭数书》中关于粟米互换的题目分别在给出粟米互换标准的第39条及第41条之下，即第40条“秏”，第42条“粟求米”，第43条“粟求米”，第44条“米求粟”，第45条“米粟并”，第46条“粟米并”。后2条在衰分术中已经谈过，此不赘。第35条之下没有粟米互换的题目。第42条“粟求米”根据第41条的粟米互换标准，给出了粟求米，粟求麦，粟求粺，粟求毇，米求粟的公式。第44条“米求粟”是：
米求粟 以米求粟，因而五之，三成一。今有米七分升六，当为粟几何？曰：为粟一升七分升三。术曰：母相乘为法，以五乘六为实。
这是很简单的题目：
升×5÷3=（6升×5）÷（7×3）=
升。
这类问题，后来发展为《九章筭术》的“今有术”。
此外，《筭数书》第50条“丝练”给出了级丝与练的互换公式：
丝练 以级丝求练，因而十二之除十六而得一。
亦即：
练=（级丝数×12）÷16。
这里级丝率16，练丝率12，与《九章筭术》均输章“今有络丝”问络丝率16，练丝率12相同。可见，《筭数书》的“级丝”应该是《九章筭术》的“络丝”。此条与粟米互换是同类的问题，但是《筭数书》没有给出相应的例题。
2.异乘同除
在中国传统数学史上，“异乘同除”是个后起的术语。明初编纂《永乐大典》，人们将《九章筭术》卷三“衰分章”后半卷及其后数学著作中同类的内容编入“筭”字条的卷16343，称为“异乘同除”。[5]《筭数书》中有十几个这类题目，我们借用“异乘同除”归纳之，并以第19条“铜秏”，第25条“息钱”，第32条“挐脂”，第33条“取程”，第34条“秏租”，第36条“取枲程”为例说明其方法。先分析后4条。“挐脂”条是：
挐脂 为挐，米一斗、水一斗半斗、
脂廿斤，为挐脂卅六斤。今有
脂五斤，问：用米、水、为挐各几何？得曰：用米二升半升，水三升四分升三，为挐九斤。术曰：以廿为法，直水十五、米十、挐卅六，以五乘之为实，实如法得水、米各一升、挐一斤。不盈，以法命分。其以挐、米、
亦一两，得
九分之五也。有米三升，问：用脂、水各几何，为挐几何？曰：用脂六斤、水四升半升，为挐脂十斤十二两十九朱五分朱一。
此条首先规定了米、水、
脂为挐脂的标准：
米 水 
脂 挐脂
1斗 
斗 20斤 36斤
然后提出了2个问题。第1个问题是：
米 水 
脂 挐脂
？ ？ 5斤 ？
显然，
米=（5斤×1斗）÷20斤=
升，
水=（5斤×
斗）÷20斤=
升，
挐脂=（5斤×36斤）÷20斤=9斤。
第2个问题是：
米 水 脂 挐脂
3升 ？ ？ ？
水=（3升×
斗）÷10升=
升，
脂=（3升×20斤）÷10升=6斤，
挐脂=（3升×36斤）÷10升=
升。
这类计算，刘徽都将其归结为今有术。第1个问题求米和水，第2个问题求脂和挐脂，《筭数书》都是用与被乘数不同单位的数乘，而用与被乘数相同单位的数除，所以后来被称为“异乘同除”。
“取程”条是：
取程 取程十步，一斗。今千之八升，问：几何步一斗？得田十二步半一斗。术曰：八升者为法。直一升步数而十之，如法一步。竞程卅七步，得禾十九斗七升。问：几何步一斗？得曰：减田一步有百九十七分步百七十三而一斗。取程五步一斗，今千之一斗一升。欲减田[3]令一升。[4]得曰：减田十一分步五。术曰：以一升数乘五步，令十一而一。
此条含有3个题目。第1题是：
田 禾 千
10步 1斗 8升(www.xing528.com)
？ 1斗
禾=（10升×10步）÷8升=
步。
第2个题目是：
田 禾
37步 19
斗
？ 1斗
田=（1斗×37步）÷19
斗=1
步。
第3题是：
田 禾 千
5步 1斗 1斗1升
？ 1升
田=（1升×5步）÷1斗1升=
步。
都是“异乘同除”类问题。《九章筭术》中没有与以上3条类似的题目。
“秏租”条是：
秏租 秏租产多千少。曰：取程七步四分步一而一斗。今千之七升少半升，欲求一斗步数。曰：九步四十四分步卅九而一斗。术曰：直十升，以乘七步四分步一，如千成一数也。程它物如此。
此条只1个问题，即：
田 禾 千
7
步 1斗 7
升
？ 10升
田=（10升×7
步）÷7
升=9
步。
也是“异乘同除”类问题。
“取枲程”条是：
取枲程 取枲程十步，三尺韦束一，今千之廿八寸，问：几何步一束？十一步有九十八分步四十七而一束。术曰：千自乘为法。生自乘，有以生一束步数乘之，为实。实如法得一。
枲，音xǐ，大麻的雄株。围是计算树木的横截圆周的单位，这里似指麻捆的圆周。题目可以表示成：
田 围（生） 围（千）
10步 3尺 2尺8寸
？ 3尺
《筭数书》给出的解法是：
步数=（3尺×3尺×10步）÷（2尺8寸×2尺8寸）=11
步。
这也是“异乘同除”类问题。不过，被除数中的被乘数与同（即除数）都是周长的平方，说明当时人们已经懂得圆柱的截面积与周长的平方成正比。
“铜秏”条是：
铜秏 铸铜一石秏七斤八两。今有铜一斤八两八朱，问：秏几何？得曰：一两十二朱半。术曰：直一石朱数为法，亦直七斤八两者朱数，以一斤八两八朱者朱数乘之，如法一朱。
此条的题目是：
铜 秏
1石 7斤8两
1斤8两8朱 ？
秏=（7斤8两×1斤8两8朱）÷1石
=（15/2斤×584朱）÷120斤=36
朱。
《九章筭术》中没有关于“铜秏”的题目，却有一个“丝耗”的题目，与此相类。
“息钱”条是：
息钱 贷钱百，息月三。今贷六十钱，月未盈十六日归，计息几何？得曰：廿五分钱廿四。术曰：计百钱一月积钱数，以为法。直贷钱，以一月百钱息乘之，有以日数乘之为实。实如法得一钱。
依术，
息=（今贷钱×月百钱息×贷钱日数）÷（百钱×月日数）
=（60钱×3钱×16日）÷（100钱×30日）=
钱。
这个题目与《九章筭术》衰分章“贷人千钱”的题设、解法类似，只是数字不同。同时，《筭数书》的“术”比《九章筭术》稍微抽象一些。按照刘徽对《九章筭术》的注解，《筭数书》的问题可以这样理解：已知贷人“百×月日数”钱一日息，问贷人“今贷钱×贷钱日数”钱，一日息多少，从而得出术文。
《筭数书》中“异乘同除”类问题共有13条，15个题目，在《筭数书》中是最多的。
3.连比例
《筭数书》中连比例问题只有一个，这就是第16条“负米”：
负米 人负米不智其数，以出三关，三税之一。已出，余米一斗。问：始行赍米几何？得曰：赍米三斗三升四分三。术曰：直一关而参倍为法，有直米一斗而三之，有三倍之而关数焉为实。
“参倍”应该指23，按术文，其算式是：
1斗×3×3×3÷23=3
斗=3斗3
升。
此算式大约是这样得出的：每关“三税之一”，就是说每关米3余2。设每关税前米为a1，a2，a3，那么每关税后米为a2，a3，b。因此，
a1∶a2=3∶2 a2=
a2∶a3=3∶2 a3=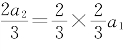
,
a3∶b=3∶2。 b=
,
由于b=1斗，于是，
a1=（b×3×3×3）÷23=1斗×3×3×3÷23.
《九章筭术》均输章有一个“持米出三关”题，与此类似。不过，那题三关所税的比例不相同。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
