《筭数书》中的衰分与返衰问题解析及问题存在部分脱误

《筭数书》有8个衰分问题，依次在第11条“共买材”，第12条“狐出关”，第13条“狐皮”，第14条“女织”，第20条“传马”，第26条“桼”，第45条“米粟并”，第46条“粟米并”；还有1个返衰问题，是第15条“并租”。此外，第21条“妇织”亦应以返衰术求解，但原术错误，此不论。

1.衰分问题

先以“狐出关”为例：

狐出关 狐、狸、犬出关，租百一十一钱。犬谓狸、狸谓狐：而皮倍我，出租当倍我。问：出各几何？得曰：犬出十五钱七分六，狸出卅一钱分五，狐出六十三钱分三。术曰：令各相倍也，并之，七，为法。以租各乘之，为实。实如法得一。

这里，犬、狸、狐以1，2，4的比例（《九章筭术》称为“列衰”，《筭数书》无此术语）分配111钱，按术文，

这完全是《九章筭术》“衰分术”的程序的应用，只是《筭数书》没有赋予“衰分术”的名称。又如“女织”：

女织 邻里有女恶自善也织，曰自再，五日织五尺。问：始织日及其次各几何？曰：始织一寸六十二分寸卅八，次三寸六十二分寸十四，次六寸六十二分寸廿八，次尺二寸六十二分寸五十六，次二尺五寸六十二分寸五十。术曰：直二、直四、直八、直十六、直三十二，并，以为法。以五尺偏乘之，各自为实。实如法得尺。不盈尺者，十之，如一寸。不盈寸者，以法命分。

依术文，解法为：

第1日织 50寸×2÷（2+4+8+16+32）=寸，

第2日织 50寸×4÷62=寸，

第3日织 50寸×8÷62=寸，

第4日织 50寸×16÷62=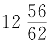寸，

第5日织 50寸×32÷62=寸。

这也是典型的衰分法。《九章筭术》衰分章衰分术的例题、《孙子筭经》卷中的题目“女子善织”问题设的数字与此题完全相同，只是文字差别较大。不过，《九章筭术》《孙子筭经》都将分数约简成以31为分母的最简分数，而《筭数书》没有约简。

“粟米并”条似有4个问题及其术，最后是抽象性术文。后2个问题脱误严重，难以校补，不论。前2个问题、术及抽象性术文是：

粟米并 米一、粟二，凡十斗，精之为七斗三分升一。术曰：皆五，米、粟并为法。五米、三粟，以十斗乘之为实。有米、粟不知数，合粟、米精之为米一斗，问：米、粟各出几何？得曰：米六升四分升之一，粟三升四分升之三。术曰：直米五升，粟五升。粟五升为米三升，并米五升者八，以为法。乃更直三升、五升，而十之，令如法，粟、米各一升。……其术曰：直米、粟，五米三粟，并，以为法。并米、粟，各乘之，为实。实如法而成一。

根据术文，第1个问题的解法是：

米 （10斗×1×5）÷[（1+2）×5]=斗，(www.xing528.com)

粟 （10斗×2×3）÷[（1+2）×5]=4斗。

第2问脱误较多，我们依意作了校补。其解法当是：

米出 10升×5÷（5+3）=升，

粟出 10升×3÷（5+3）=升。

此条中最后的术文，虽不是衰分术的一般性、抽象性术文，却是“粟米并”类问题的抽象性术文。前2个题目中的术文是这条抽象性术文的具体应用。

2.返衰问题

《筭数书》第15条“并租”是一个返衰问题：

并租 禾三步一斗，麦四步一斗，荅五步一斗。今并之，租一石，问：租几何？得曰：禾租四斗四十七分十二，麦租三斗分九，荅租二斗分二十六。术曰：直禾三步，麦四步，荅五步。令禾乘麦为荅实，麦乘荅为禾实，荅乘禾为麦实，各副直之。以一石各乘之，为实。并诸实，四十七，为法而一斗。

依术文，求禾、麦、荅租的方法是：

禾租 （4×5×10）÷（4×5+3×5+3×4）=斗，

麦租 （3×5×10）÷（4×5+3×5+3×4）=斗，

荅租 （4×3×10）÷（4×5+3×5+3×4）=斗。

这恰恰是《九章筭术》“返衰术”的应用，列衰为3，4，5。按照刘徽对返衰术的注解，

禾租（10斗×）÷（），

应用齐同术，便化成《筭数书》的算式。麦租、荅租亦如是。

《筭数书》9个衰分类问题的解法都是正确的，然而没有给出《九章筭术》“衰分术”与“返衰术”那样抽象性的一般公式。