社会网络的形式化表达：研究成果

从数学角度上讲，有两种方法可以描述社会网络：社群图法和矩阵代数方法。社群图记法常常应用于对结构对等性（structural equivalence）和块模型（block model）的研究。代数学记法可用于分析角色和关系。当然，其他统计方法也可以用来描述社会网络。

社群图（sociogram）是由莫雷诺最早使用的，现已在社会网络中得到广泛使用。用来表达一种关系的矩阵叫做社群矩阵（socimatrix）。社群图主要由点（代表行动者）和线（代表行动者之间的关系）构成。社群图中的点集可以表示为N={n₁，n₂…n_g}。这样，一个群体成员之间的关系就可以用一个由点和线连成的图表示。

如果根据关系（线）的方向，可以分为“有向图”（directed graph）和“无向图”（undirected graph）。无向图是从对称图中引申出来的，它仅仅表明重要关系的存在与否。如果关系是有方向的（例如借款关系、权力关系等），也就是说，n₁到n₂的关系与n₂到n₁的关系是不同的，那么，就应该用有向图（di_- rected graph）来表示。我们用L代表有向线的集合，用1代表其中的单条线，用箭头代表关系的方向。图5-1所示为一个简单的有向图。

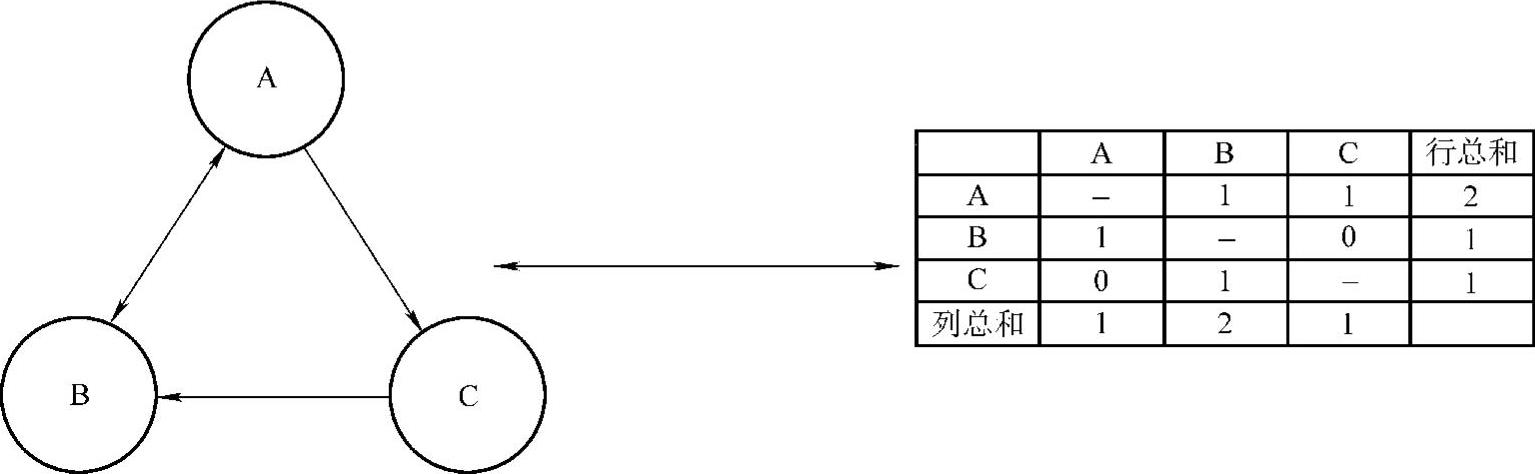
图5-1 一个有向图及其邻接矩阵

利用社群图表达关系网络的一个优点是比较清晰、明确，社会行动者之间的关系一目了然。但是，如果社群图涉及的点很多，那么图形就相当复杂，如图5-2所示，很难分析出关系的结构，这是社群图的一个缺点。在这种情况下，我们最好利用矩阵代数（matrix algebra）记法表达关系网络，用来研究多元关系，研究两种关系或者多种关系的“叠加”。假设我们已经研究了两种关系：“是朋友”、“是敌人”，那么，我们就可能研究“是朋友的敌人”这种关系。这种方法最先由H.White和J.P.Boyd提出来。

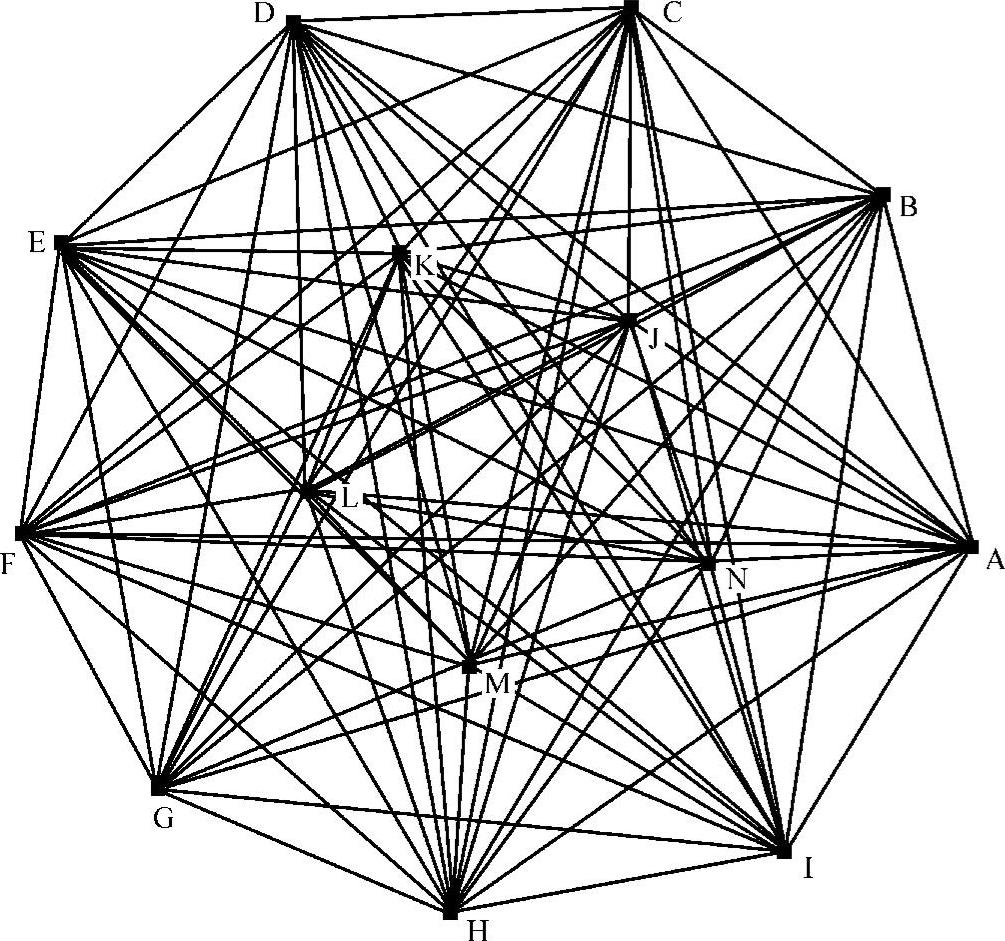
图5-2 社群图举例

如果行和列都代表来自于一个行动者集合的“社会行动者”，那么矩阵中的要素代表的就是各个行动者之间的“关系”。这种网络是1-模网络。如果行和列代表来自两个行动者集合的“社会行动者”，那么矩阵中的元素分别代表的就是两个行动者集合中的各个行动者之间的“关系”，这种网络是2-模网络。如果“行”代表来自一个行动者集合的“社会行动者”，“列”代表行动者所属的“事件”，那么矩阵中的元素就表达行动者隶属于“事件”的情况，这种网络也是2-模网络，具体地说是“隶属关系网络”。

总之，如果没有数学工具（图论、矩阵代数）的支持，社会网络分析就不可能取得重要进展。在表达关系数据的时候，社会网络分析者主要利用数学领域中的两种工具：社群图和矩阵代数。当然，社会网络方法论上的突破也离不开统计技术的发展。拥有了这两种工具，我们就能够计算一些网络测度（例如密度、点入度等）的。

在社会网络中，与“关联性”密切相关的研究是行动者之间的距离。有的行动者可能与网络中的任何一个人都建立了联系，与其他人的距离都很“近”。

有的人可能交往比较少，相对“孤立”一些。如果行动者之间的距离不一样，我们就可能找到这些行动者在网络意义上的社会分层来，也可能有助于我们理解社会群体的“同质性”、“团结性”等特点。(www.xing528.com)

下面将介绍几种距离相关的概念，并用这两种工具阐述它们在社会网络分析中所代表的含义。

（1）点的度数。与某点相邻的那些点称为该点的“邻点”（neighborhood），一个点n_i的邻点的个数称为该点的“度数”（nodal degree），记作d（n_i），也叫关联度（degree of connection）。这样，一个点的度数就是对其“邻点”多少的测量。实际上，一个点的度数也是与该点相连的线的条数。如果两个点由一条线相连，称这两个点是“相邻的”（adjacent）。“相邻”是对两个行动者直接相关的图论表达。如果一个点的度数为0，称之为“孤立点”（isolate）。点的度数测量了行动者参与活动的情况，它是测量“中心度”的基础。

这个概念在对有向图的分析时需要做些调整。在一个有向图中，必须考察线的方向。因此，一点的“度数”包括两类，分别称为点入度（in-degree）和点出度（out-degree）。一个点的点入度指的是直接指向该点的点的总数；点出度指的是该点所直接指向的点的总数。因此，点入度用一个有向图矩阵的列总和表示，点出度用行总和表示。例如，在图5-1中，点B的列总和为2，因为它“收到”了两条线。但是，B的行总和只是1，因为它只向外发出一种关系。相应的社群图则清楚地显示出它的点入度为2。

（2）测地线。在给定的两点之间可能存在长短不一的多条途径。两点之间的长度最短的途径叫做测地线。如果两点之间存在多条最短途径，则这两个点之间存在多条测地线。

（3）距离。两点之间的测地线的长度叫做测地线距离，简称为“距离”（distance）。也就是说，两点之间的距离指的是连接这两点的最短途径的长度。我们把点n_i和n_j之间的距离标记为d（i，j）。如果两点之间不存在途径（即二者之间是不可达的），则称二者之间的距离是无限的（或者无定义）。如果一个图是不关联图，那么其中至少有一对点的距离是无限的。

（4）直径。一个图一般有多条测地线，其长度也不一样。我们把图中最长测地线的长度叫做图的直径。如果一个图是关联图，那么其直径可以测定。如果图不是关联的，那么有的点对之间的距离就没有界定，或者就距离无穷大。在这种情况下，图的直径也是无定义的。

（5）密度。这个概念是为了汇总各个线的总分布，以便测量该分布图与完备图（complete graph）的差距有多大。固定规模的点之间的连线越多，该图的密度就越大。具体地说，密度指的是一个图中各个点之间联络的紧密程度。

（6）权力和中心性。“权力”是社会学中的一个重要概念。从社会网络的角度对权力的这种界定可以进一步体现在网络研究者对权力的各种定量表述上。也就是说，网络分析者是从“关系”的角度出发定量地界定权力的，并且给出多种关于社会权力的具体的形式化定义，即各种中心度和中心势指数。这可以看成是网络分析者的独特贡献，因为网络研究者更倾向于用“中心性”表达权力概念。

“中心性”是社会网络分析中的重点之一。个人或者组织在其社会网络中具有怎样的权力，或者说居于怎样的中心地位，这一思想是社会网络分析者最早探讨的内容之一。这个观点最初体现在社会计量学的一个重要概念—“明星”（star）中。所谓明星指的是那个在其群体中最受关注的中心人物。巴乌拉斯最先对中心度的形式特征进行了开创性研究，验证了如下假设：即行动者越处于网络的中心位置，其影响力越大。研究发现，中心度与群体效率有关，也与参与群体的个人的满意度有关。随后的学者利用这个概念解释复杂的社会系统。

在社会网络分析中对权力的探讨集中体现在对“中心度”和“中心势”的量化分析上。常用的中心度和中心势指数包括：点度中心度、中间中心度、接近中心度、特征值中心度以及伯纳西茨权力指数，还有与它们对应的中心势指数。中心度刻画单个行动者在网络中所处的核心位置；中心势刻画的则是一个网络所具有的中心趋势。假设研究点度中心性，那么对于一个拥有n个行动者的网络来说，其中可以计算出来的中心度指数有n个，但是计算出来的中心势指数只有一个。

“点度中心度”刻画的是行动者的局部中心指数，测量网络中行动者自身的交易能力，没有考虑到能否控制他人。“中间中心度”研究一个行动者在大多程度上居于其他两个行动者之间，因而是一种“控制能力”指数。“接近中心度”考虑的是行动者在大多程度上不受其他行动者的控制。如果网络中的一个行动者在交易的过程中较少依赖于他人，此人就具有较高的中心度。一个点越是与其他点接近，该点就越不依赖于他者。刻画一个行动者的特征向量中心度是为了在网络总体结构的基础上，找到最居于核心的行动者，而不关注“局部”的模式结构。对中心度的测量不能脱离其他点的中心度。因此，在计算中心度的时候包含着内在的循环。