基本公式修正-在线分析样品处理技术

（1）样品通过处理部件的时间Tt2

样品处理部件包括阀门、过滤器、气液分离器、旋风分离器、样品冷却器等。样品在这些部件中的传送，并非是一个纯容积滞后过程，还存在一个浓度变化滞后问题，这是由于样品组成发生变化时，新进入的样品与滞留在部件中的老样品混合平均所造成的。新样品将混合样品

逐步置换完毕需要一段时间，这段时间远比Tt2=要长。可以把样品处理部件看成一个阻容环节，即一阶滞后环节，其表达式为

式中　C——样品组成发生阶跃变化后的浓度；

y——处理部件出口浓度；

T——时间常数，即y=63.2%C时的时间，通常令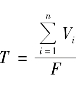，即取纯容积滞后时间为T；

t——浓度变化滞后时间。

由式（4-5）可求得

当t=T时，y=63.2%C；

当t=2T时，y=86.5%C；

当t=3T时，y=95%C；

当t=4T时，y=98.2%C；

当t=5T时，y=99.3%C。(www.xing528.com)

可见当t=5T时，浓度置换才接近全部完成，通常取t=3T，即出口浓度变化到95%C时，即认为样品已通过该部件（图4.1）。

由此可见，样品处理部件的传送滞后时间是相当大的，其容积越大，滞后时间越长。例如，一个0.5 L的气液分离罐，其容积仅相当于40 m长φ6 mm×1 mm的管子，但其传送滞后时间则相当于样品通过40×3=120 m长管子所需时间。因此，在设计样品系统时，应尽可能减少处理部件用量，尽可能采用小容积的部件。

对基本公式中Tt2=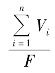项作如下修正：

（2）样品通过传送管线的时间Tt1

图4.1　样品浓度阶跃变化时的一阶滞后效应

样品传输管线由管子和接头组成，与Tube管等内径的球阀、闸阀等也可以包括在内。这里还存在着一个死体积问题。所谓死体积，是指只有一端与流动系统相连通的体积，所有管接头和等内径阀门都有死体积，管线的死端更是明显的死体积。死体积和样品处理部件一样，也存在浓度变化滞后问题，二者不同之处是：处理部件通过均匀混合逐步完成样品置换，而死体积与流动样品通过扩散和湍流发生交换，最后被新样品填满，死体积也可看作一阶阻容环节，只是置换速度较样品处理部件还要缓慢，但由于体积很小，其影响也较小。实际计算时，可根据样品管线死体积数量的多少，用一个经验系数对传输时间加以修正：

（3）修正后的基本公式

将式（4-6）、式（4-7）代入式（4-4）：