偶极子理论模型与计算

s-SNOM相关的理论研究主要关注入射光波与探针和被测物质的近场耦合与散射,其中的一个重点是针尖的散射增强效应。针尖的局域场增强过程主要有局域场表面等离激元共振效应、避雷针效应、电场梯度效应和镜像偶极子效应。为了便于理解和分析s-SNOM系统的工作机理与特点,主要介绍镜像偶极子效应的理论模型。

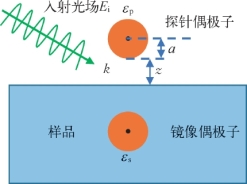
图7-18　镜像偶极子理论模型

镜像偶极子理论模型如图7-18所示。在入射光场的所用下,探针针尖的局域场限制在针尖和样品的间隙处,产生显著的增强效应。为了更加直观地分析针尖与样品的近场耦合和散射增强效应,将探针针尖简化为一个偶极子。针尖与样品产生的耦合,可以看作是探针偶极子在样品中诱导产生了一个镜像偶极子。设探针针尖的曲率半径为a,介电常数为εt,样品的介电常数为εs,只考虑垂直于样品表面的入射光电场分量,则探针的极化率αt为

样品的极化率αs为

考虑到镜像偶极子与探针偶极子的近场耦合作用,修正后的探针极化偶极矩为

式中,r=a+z;p′=αsp,p=αtE i。由于耦合系统的总电场是探针偶极子和镜像偶极子电场的叠加,因此耦合系统的有效极化率为(www.xing528.com)

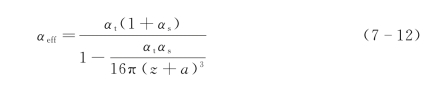
从公式(7-12)可以看出,当针尖靠近样品表面时,在入射光场作用下,整个耦合系统的有效极化率受针尖-样品系统之间距离z和针尖曲率半径a的影响。通常在有样品的情况下,局域场增强效果会更加明显,这种增强效应使得局域电场的分布集中在针尖与样品的间隙处,由于针尖曲率半径可以做到纳米量级,因此通过采用更细的针尖可以实现更高的空间光谱分辨率。

为了获得纳米量级的分辨率,探针针尖的曲率半径一般会远小于入射光波长,因此可采用Mie散射理论计算探针针尖的散射截面:

在s-SNOM系统中,当外部激光聚焦入射到针尖位置时,由于聚焦光斑相对于针尖曲率半径来说要大得多,聚焦光斑中有很大一部分光打在探针轴和样品表面上,因此探测器收集到的信号不仅包括从针尖散射的近场信号,也包括从样品表面和探针轴散射的远场背景信号。由于远场背景信号中不包含样品的近场光学信息,而且此信号强度远远大于近场散射信号,因此直接利用散射信号扫描成像很难提取样品表面的光学信息。为了减少远场背景信号的干扰,s-SNOM系统中的AFM工作在轻敲模式下。在轻敲模式下,探针间歇式地靠近和远离样品,设此轻敲频率为Ω,则从针尖散射的信号和探针轴表面散射的信号同时被调制,而从样品表面散射的信号调制较少,采用这种方法可以有效地减少来自样品表面散射信号的干扰。近场散射信号随着探针-样品之间距离的增大呈非线性的快速衰减,而来自探针轴散射的背景信号则与探针-样品之间的距离呈线性关系。对探测器收集到的散射信号进行傅里叶级数展开,其零阶直流分量中绝大部分是背景信号,一阶分量中既有近场信号又有背景信号,而在高阶分量中背景信号已消除,因此采用高阶解调的方法,可以有效压制背景信号,提取所需的近场信号。使用MATLAB计算高阶解调信号随探针-样品之间距离增大时的变化曲线,结果如图7-19所示。

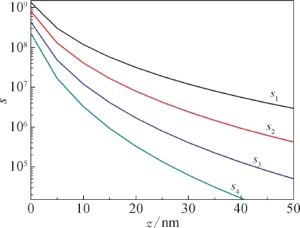
图7-19　高阶解调信号随探针-样品之间距离增大时的变化曲线

从图7-19可以看出,随着解调阶次的增加,近场散射信号强度逐渐变小,背景信号抑制效果变好,系统成像的分辨率也越来越高。因此为了提取散射信号中的近场信号,同时获得较好的信噪比,当照明光源在可见光波段时,一般采用三阶解调的方式。