基于等离激元超表面的偏振转换研究成果

自然界中的各向异性材料,即传统的各向异性介质由于不同方向折射率的差异被广泛应用于偏振片实现线极化、圆极化、交叉极化之间的相互转换。但是,在传统的偏振转换手段被用来设计制作偏振转换器的过程中,为了满足一定的相位差往往要求有很大的厚度,而且工作频宽也由于材料本身而受限。新型人工电磁材料的提出减小了传统各向异性材料制造的难度,为各种偏振调制提供了新的手段和方法。电磁超材料实现线偏振转换成圆偏振的手段可分为透射式偏振转换和反射式偏振转换。透射式偏振转换,不仅要求不同偏振方向的透射波产生一定的相位差,同时还要保证它们透过的振幅相同。同时,透射式偏振转换的转换效率与单元结构的谐振有很大联系,利用率较低。对于反射式偏振转换,只要保证材料无损耗或者损耗比较低,在一定的频率上,就可近似认为电磁波实现了全反射,转换效率接近100%。此时,反射系数均为1,只需要满足特定的相位差就可实现高效率的偏振转换。通常各向异性新型人工电磁材料的相对介电常数和磁导率为

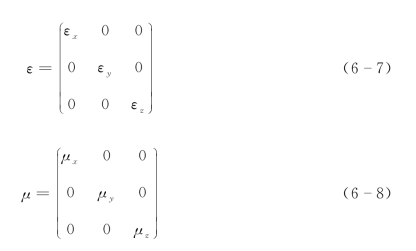
式中,对角线元素可为正值也可为负值。在各向异性介质中,电场方向和其产生的偏振方向不一致,即D与E的方向不一致,称为电各向异性的介质;同样地,若B与H方向不一致,称为磁各向异性的介质。

假设一束平面电磁波以x极化沿+z方向入射到各向异性介质中,即

根据麦克斯韦方程组,在无源的空间里:

代入E可以得到

将式(6-11)代入式(6-14)得到

由以上结果可见,当电磁场入射到各向异性介质时,如果μxεy≠μyεx,则电场x方向和y方向所得到的波矢量不同,那么对于给定厚度的各向异性介质来说,这两种情况下的入射波将会得到不同的相位。这就是各向异性对电磁波极化进行调制的基本原理。电磁超材料的深入研究为新型各向异性材料的发展提供了新的有效出路。各向异性这一优良特性和电磁超表面相结合,从而使得超表面具有很强的偏振调制能力。超表面(Metasurface)是一种由一系列的亚波长的人工微结构构成的超薄二维阵列平面,其本质是具有亚波长周期性的不连续相位光栅。超表面通过控制波前相位、振幅以及偏振态来实现对光束的控制。2011年,Yu等提出如果在两种介质的分界面上能够产生一个随位置变化的突变相位,那么就可以通过精确设计散射结构对经过界面的散射电磁波进行相位调制,从而实现反常折射和反射。因此,他们将超表面定义为能够使一束光在自由空间波长范围内产生相位、振幅突变效应的超薄平面光学元件。由亚波长的人工微结构(亦可称为等离子体天线)序列组成的超表面具有制作相对简单、损耗相对较低、体积小型化和厚度超薄等特点,其可实现对电磁波振幅和相位、传播模式、偏振态的有效调控。

2012年,Yu等又利用V形天线组成的超表面结构实现了1/4波片的功能,如图6-4所示。所提出的超表面结构是由两个具有不同相位突变分布的子单元a和子单元b构成的,每个子单元包含8个V形金属天线。当一束线偏振波垂直经过两个子单元构成的表面后,可产生两束具有相同振幅、偏振方向相互垂直的同向波。当子单元内的V形金属天线的间距设定为周期尺寸的1/4时,所产生的同向波相位差恰好为π/2,再经过干涉叠加形成一个圆偏振光。又由于该超表面具有反常折射的性质,所形成的反常折射光恰好满足线偏振向圆偏振转化的条件。

(www.xing528.com)

图6-4　V形天线超表面结构示意图

对于电磁波偏振态的转换,我们可以通过对入射电磁波进行分解,将对应的电磁波分量的相位进行转换,从而实现电磁波偏振态的转换。例如,圆偏振态的获取,我们可以通过两束偏振方向垂直、相位差为π/2的线偏振叠加来实现,那么我们只需要设计可以获得我们预期想要的相位的方法即可。超表面可使入射的电磁波发生相位突变,通过修改超表面结构单元的几何尺寸,则可获得任意相位。其中对于圆偏振光入射,只需要控制超表面结构单元的光轴方向就可实现相位的调控。因为超表面具有空间变化的光轴,所以会产生PB(Pancharatnam-Berry)相位。由于PB相位仅与光轴的方向角有关,又被称为几何相位。PB相位对于圆偏振光的调控相当重要,到目前为止关于圆偏振光的调控都是通过PB相位来实现的。

对于任意的超表面来讲,假定其位于直角坐标系的z=0平面内,可定义一个一般形式的透射矩阵:

式中,T xx代表y方向的线偏振光入射时x方向的透射系数,其他元素的意义类推。对于超薄的超表面来说,当入射光斜入射时可能打破二维表面的对称性进而产生磁耦合效应导致T xy≠T yx,即使有磁耦合效应存在,这种效应也是可以忽略的。特别地,在垂直入射的情况下,x与y偏振之间是没有耦合的,即T xy=T yx=0。对于光轴与x轴成θ角的超表面结构单元而言,其透射矩阵在直角坐标系中表示为

为了探讨圆偏振光入射到超表面后其透射光的特性,我们先讨论右旋圆偏振光入射的情况。我们用琼斯矢量E in表示入射的右旋圆偏振光。在以两种圆偏振光为基准的坐标系中,右旋圆偏振光的琼斯矢量可以表示为E in=E 0·[1,0]T,因此透射光可以表示为

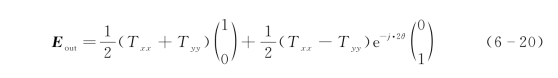
同理,对于左旋圆偏振光的情况,入射光的琼斯矢量表示为E in=E 0·[1,0]T,此时出射场可表示为

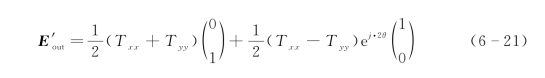
式(6-20)和式(6-21)中的2θ为交叉偏振光所携带的PB相位。从式(6-20)可以看出圆偏振光入射时,透射光包含两部分:不携带额外相位的相同偏振的偏振光(方程中的第一项)以及具有额外相位2θ的交叉偏振光(方程中的第二项)。需要注意的是方程中的透射系数都是复数,既有振幅信息又有相位信息。我们考虑一种特殊的情况,当T xx与T yy之间的相位差为π时,式(6-20)中的第一项为零。此时,透射光中将只含有交叉偏振光,即偏振转化效率为100%。从推导过程可得出要实现预期的相位变化,只需要简单旋转相应的角度就可获得想要的相位。在设计线偏振变圆偏振的超表面转换器时,我们可以考虑将线偏振光分解为一束左旋圆偏振光和一束右旋圆偏振光,利用PB相位实现圆偏振光的相位突变,从而可以将线偏振光转换为圆偏振光。

基于超表面的THz波线偏振转换器是一种超薄的人工微结构波片/器件。由于它所具备的调控偏振的功能可以广泛应用于成像、探测、传感以及信号处理等领域,因此,近几年已经引起了研究热潮。

目前已提出的超表面线偏振转换器有许多种,按照其实现频率的范围可以分为单频线偏振转换器、多频线偏振转换器和宽频线偏振转换器等;按照其结构类型可以分为金属线栅结构线偏振转换器、垂直金属缝结构线偏振转换器和非对称结构线偏振转换器;按照层数可以分为单层线偏振转换器、双层线偏振转换器和多层线偏振转换器。下面我们将介绍基于单层超表面和非对称性原理而设计的分裂双环槽结构的宽频THz波线偏振转换器。