太赫兹螺旋形SLSPs及应用

在图5-3所示的散射截面谱中,除了电谐振以外,还存在谐振频率非常接近的磁谐振,但由于磁谐振非常微弱,所以并没有在图5-3中显示出来。根据式(5-14),如果想将电谐振和磁谐振的共振频率区分开,可以增加结构中的填充介质的折射率n g,还可以延长槽的长度。我们设计的螺旋形结构SLSPs可以同时激发电谐振和磁谐振。

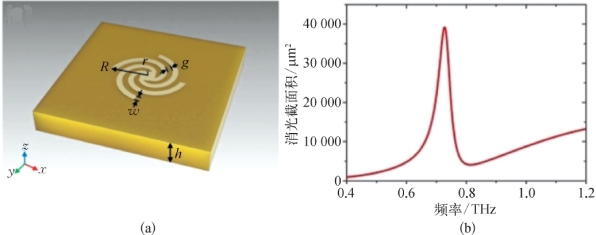
图5-17

(a)螺旋形金属盘结构示意图;(b)电磁波垂直入射时,螺旋形金属盘的消光截面积

螺旋形金属盘结构如图5-17(a)所示,其基底为20μm厚的聚酰亚胺(介电常数为3,损耗角正切值为0.03)。螺旋形金属薄膜为金膜,厚度为200 nm,螺旋形结构由内半径r=6.5μm的中心圆盘和外半径R=33μm的四个螺旋形臂组成,四个臂之间的间隔宽度g=5μm,每个臂的宽度w=5μm。图5-17(b)为该结构在频域模式下的消光截面积的仿真结果。在仿真实验中,采用频域求解器进行仿真,光源设置为沿轴极化的平面波并且垂直入射该结构,x、y、z边界都设置为开放边界条件。从图中可以明显看出曲线在0.73 THz处有一个明显的谐振峰。

为了研究该频点的物理机制,图5-18(a)给出了0.73 THz处结构正上方5μm处的垂直电场(E z)分布的仿真结果。结果表明,在结构左右两端电场强度最强,与传统的光波段LSPs偶极子谐振场型一致。图5-18(b)仿真了金属盘在0.73 THz处发生谐振时,y=0截面内的电场强度和电场线分布。电场线始于结构的左端,终于结构的右端,并且结构左右两端的电场强度是最强的,结果符合一个电偶极子的电场线分布。该电场线分布与电偶极子的电场线分布相似,说明在0.73 THz处发生了电偶极子谐振,这证明了该结构能够在THz波段支持SLSPs。

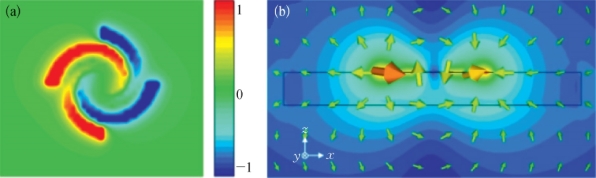
图5-18

在0.73 THz处,结构正上方5μm处的垂直电场(E z)分布(a)和y=0截面内的电场强度和电场线分布(b_________________________________________________________________________________)

此外,当螺旋形金属盘外半径R=33μm时,螺旋形金属盘对应的谐振波长为412μm,远大于结构的外半径尺寸。如果只改变螺旋形金属盘的外半径R(29～37μm),则螺旋形金属盘的消光截面积与外半径R之间的关系如图5-19(a)所示。随着螺旋形金属盘的外半径R逐渐变大,谐振峰位置会逐渐向低频移动(谐振波长逐渐增加)。图5-19(b)给出了螺旋形金属盘的外半径R与谐振波长之间的关系。从图中可以看出,螺旋形金属盘外半径R与谐振波长呈线性关系,具体来说,当外半径从29μm增大到37μm时,对应的谐振波长从319μm增大到520μm,外半径和谐振波长之比从9.1%下降到7.1%,结构的亚波长程度也将逐渐加大。

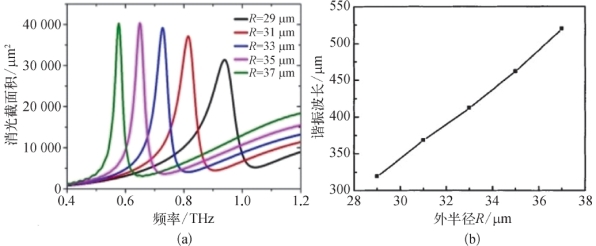
图5-19

(a)不同外半径的螺旋形金属盘的消光截面积;(b)螺旋形金属盘的外半径R与谐振波长之间的关系(www.xing528.com)

对于具有周期结构的螺旋盘,采用图5-17(a)中的螺旋形金属盘结构参数,通过改变周期p的大小(其他参数保持不变),研究相邻单元之间由于存在耦合效应所导致的SLSPs的谐振频率的偏移现象。当周期p从80μm到180μm、间隔为20μm变化时,其透射谱的变化如图5-20(a)所示。当阵列周期p从180μm减小到100μm时,SLSPs的谐振频率逐渐增加。当阵列周期p从100μm减小到80μm时,谐振峰发生红移,谐振频率向低频大幅偏移,且在80μm处的谐振频率小于180μm的谐振频率。以上结果说明,谐振单元之间的耦合分为两种:当周期较大时,偶极子谐振的辐射在单元之间相互耦合中占主导作用;当周期较小时,单元之间的相互作用主要是由静态偶极子耦合引起的。当阵列周期大于100μm时,结构谐振频率的蓝移主要是由偶极子谐振的辐射导致的;当阵列周期小于100μm时,静态偶极子耦合导致结构谐振频率的红移。为了验证周期调控特性,图5-20(b)给出了样品的透射谱测试结果(样品的大小均为15 mm×15 mm,插图为周期p=180μm的样品实物图和光学放大镜拍摄样品图)。实验结果与仿真结果高度吻合,证明了SLSPs谐振单元周期的变化对其谐振频率有着较大的影响。

当平面波垂直入射时,在消光截面谱图中只出现一个谐振峰,对应于SLSPs的电谐振模式。而当平面波从水平入射激发时,螺旋形金属盘的电磁响应会有所不同。按照5.3.1节中的盘结构参数,平面波从水平入射时[图5-21(a)中插图],螺旋形金属盘的消光截面积曲线如图5-21(a)所示。水平入射时的消光截面积曲线出现了两个谐振峰,频率分别为0.73 THz和1.06 THz。其中第一个谐振峰的位置与图5-17(b)中所示的谐振位置都是在0.73 THz处,这表明此谐振都是由电偶极子谐振导致的。接着,通过图5-21(b)所示的结构正上方5μm处的垂直磁场(H z)分布来确定第二个谐振峰(1.06 THz处)的谐振模式。结果表明当谐振发生时,中心结构处磁场最强,而且整个结构表面相位分布一致,磁场谐振方向沿着z方向。为了进一步确定谐振模式,图5-21(c)给出了螺旋形金属盘在1.06 THz处发生谐振时,y=0截面内的磁场强度和磁场线分布。从图中可以看出,在谐振发生时,磁场线从结构中心处穿过结构形成一个闭环回路。该磁场线分布与一个沿着z方向的磁偶极子的磁场线分布十分吻合。以上结果表明,螺旋形金属盘在1.06 THz处发生了磁偶极子谐振。

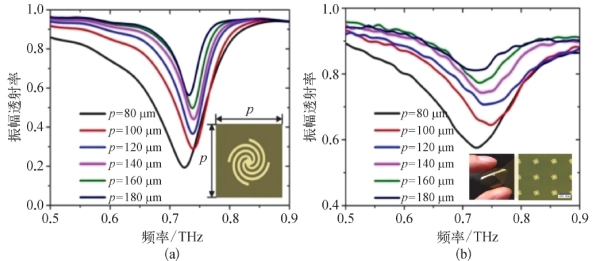
图5-20

(a)不同周期的螺旋形金属盘阵列的透射谱仿真结果;(b)不同周期的螺旋形金属盘阵列的透射谱实验图,插图为加工样品的实物图

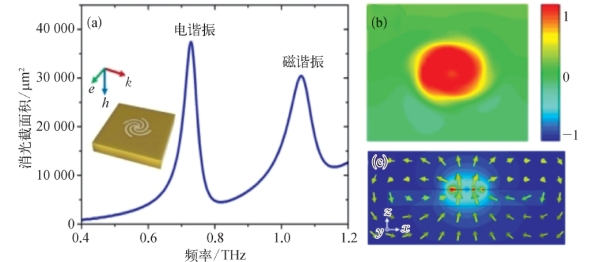
图5-21

(a)平面波从水平入射时,螺旋形金属盘的消光截面积;(b)1.06 THz时,结构正上方5μm处的垂直磁场(H z)分布;(c)1.06 THz时,y=0截面内的磁场强度和磁场线分布

由图5-17(b)和图5-21(a)可以看出,磁谐振在THz波垂直入射条件下无法激发,而水平入射激发磁谐振在实验上又难于实现。但我们可以采用5.3.1节中的方法,利用明态的偶极子模式激发暗态的磁谐振模式,如图5-22(a)中插图所示。这里明态的偶极子结构选用长度为90μm、宽度为5μm的金属条。图5-22(a)中黑线和图5-22(c)中的电场分布确认了在1.06 THz处的模式为激发的金属条偶极子模式。这样我们可以采用与5.3.1节中类似的方法,将金属条与螺旋形金属盘组成复合结构,仿真结果和实验结果均发现在1.06 THz处出现了一个透明的窗口。图5-22(d)中的电场分布表明,当THz波从正上方入射时,这种复合结构确实可以激发暗态的磁谐振模式,其物理机理为太赫兹波首先激发金属条的偶极子模式,再通过偶极子模式以近场方式激发暗态模式,即被金属条的偶极子模式间接近场激发。而激发的磁谐振会抑制金属条的偶极子谐振,导致在1.06 THz处出现了一个透明的窗口。

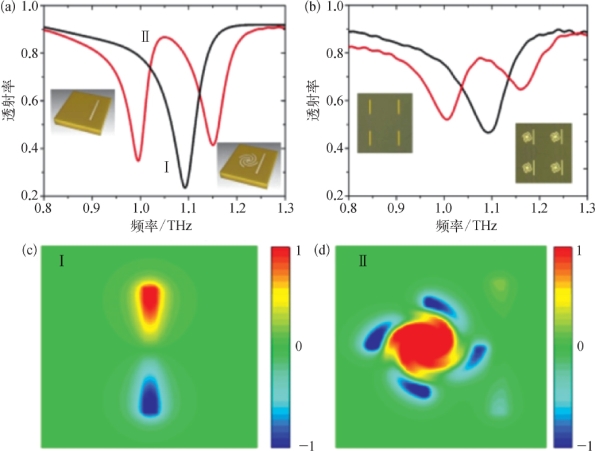
图5-22　金属条和复合结构的仿真(a)和实验(b)透射谱以及在1.06 THz处金属条(c)和复合结构(d)的电场分布