太赫兹表面等离激元的SLSPs现象

在低频波段,首先在二维周期开槽金属圆柱体上发现了SLSPs。如图5-2(a)所示,该二维结构是由在一个圆柱体外围刻蚀的多个凹槽组成的。其内圆柱的半径为r,外围由N个深度为R-r且宽度为a的凹槽构成。在二维结构的凹槽内填充介质,介质的折射率为n g。图5-3(a)(b)分别为二维周期开槽金属圆柱体和等效人工电磁圆柱体的散射截面积随归一化频率变化的关系,两者有着非常相似的散射曲线,都可以在曲线中看到多个谐振峰;右侧列出了各谐振点的磁场H z的分布情况,可以看到两者的谐振模式几乎没有差别。

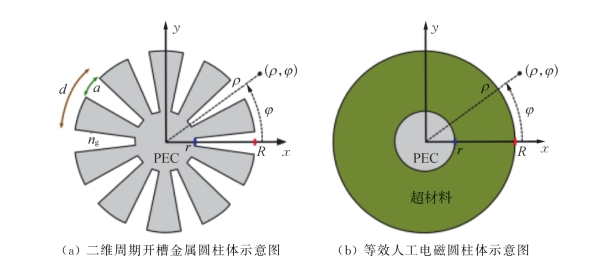
图5-2

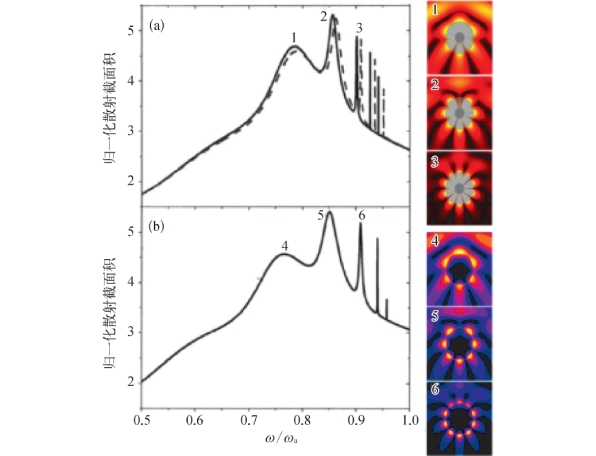
图5-3

(a)二维周期开槽金属圆柱体的散射截面积;(b)等效人工电磁圆柱体的散射截面积:右侧插图为两种金属圆柱体发生谐振时的磁场H z的分布图

金属在光频段下会呈现一种等离子体的形态,所以金属圆柱体的散射截面可以清楚地表明金属表面上的局域表面等离激元的谐振特性。对于太阳花结构来说,当波长远大于其外部凹槽的周期时,可以将外部的凹槽看作一层厚度为h=R-r的人工电磁介质层。这种人工电磁介质层在低频波段具有等离子体性质。当电磁波为沿着z方向的磁场(TM波)时,假定金属在低频波段呈现完美电导体的特性,即在外围凹槽处,Eρ=E z=0,Hφ=0,此时周期凹槽对应的新型人工电磁介质层的本构参数为ερ=εz=0、εφ=0。根据等效介质理论,将亚波长凹槽等效为各向异性材料,则电磁波在凹槽中沿着z方向和ρ方向的传播速度等于c/n g,对应的人工电磁介质层满足条件,即μρ=μz=a/d,此时各向异性新型人工电磁介质层的介电常数为εφ=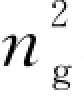d/a。圆柱体上周期凹槽的截止频率由槽深h和填充折射率n g决定:

包裹着介质的二维圆柱体的总散射截面积可以由Mie散射理论得出:

其中,

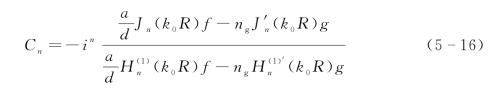
通过式(5-15)求得的包覆等效人工电磁介质层的金属圆柱体的散射截面积结果如图5-3(a)中虚线所示。理论计算的散射截面积结果和使用COMSOL Multiphysics仿真的结果基本一致,并且其电磁散射响应与传统LSPs相似。因此将这种在低频波段下利用周期开槽的超材料结构实现的谐振模式称为SLSPs谐振。即使当圆柱体的高度很小(超薄)时,谐振模式仍然存在。这种超薄结构促进了THz频段SLSPs的研究。下面我们介绍在THz频段SLSPs的激发方法和谐振特性。

(1)C型谐振器激发

本小节我们分析在THz频段的超薄褶皱金属圆盘(Corrugated Metallic Disk,CMD)上正常入射时的透射光谱。图5-4(a)为CMD的几何结构,外圆盘半径R=150μm,内金属圆盘半径r=60μm,金属圆盘由周期d=2πR/N的金属凹槽包围,其中周期数量N=36。参数α=a/d=0.4是单个周期性结构中的空气填充率。金属薄膜(铝,电导率σAl=3.56×107S·m-1)圆盘的厚度t=200 nm。衬底为25μm厚的聚酰亚胺(PI),介电常数为3.5,损耗角正切值为0.05。使用常规光刻技术[几何参数选择与图5-4(a)相同]制作样品,图5-4(b)为样品的扫描电镜图。利用THz-TDS系统测量该样品的透射光谱,如图5-5(a)所示(仿真结果也在图中显示用于比较)。在理论和实验上都观察到在0.35 THz处只有一个共振。图5-5(c)中电场分布表明这种共振是偶极子模式。由图5-3所知,CMD结构的散射截面谱中存在多个散射谐振峰(表明多极子共振),这是由掠入射激发的平面波引起的。从实验的角度来看,由于缺乏合适的太赫兹光源可以以高耦合效率掠入射激发暗态的多极子,在太赫兹频率下通过掠入射验证SLSPs模式在技术上是困难的。

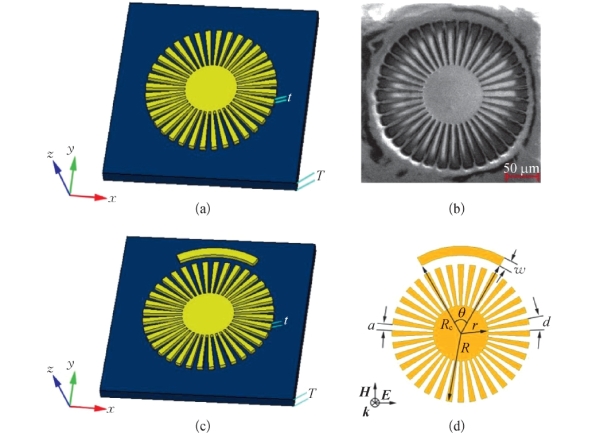
图5-4

(a)CMD的几何结构(具有内金属圆盘半径r=60μm和外圆盘半径R=150μm的金属铝膜圆盘、基于厚度T=25μm的PI介电衬底,周期数量N=36,周期长度d=2πR/N,槽宽a=0.4d,金属铝膜圆盘的厚度t为200 nm);(b)扫描电镜图;(c)混合结构三维图;(d)混合结构中的参数示意图

为了在正入射角下激发多极子共振,我们打破褶皱金属圆盘结构中的对称性。首先,提出了由一个CMD和一个C形谐振器(C Shaped Resonator,CSR)组成的混合结构。图5-4(c)(d)为CMD和CSR混合结构的示意图,其中CSR的张角为θ,内半径为R c,宽度为w,CMD和CSR之间的间隙宽度g=R c-R。

这种混合结构可以激发SLSPs模式,透射光谱如图5-6(a)(b)所示(θ=60°,w=10μm)。理论上可观测到明显的多极子共振(用C1～C5标记),并且这些共振(C1～C4)大多数可通过实验观察到。较高的谐振谷(用M标记)代表CSR的本征偶极子模式。图5-6(c)给出了与振荡C1～C5相对应的电场分布,这表明明态的CSR可以激发暗态的多极子共振。激发多极子共振具有重要的意义,通过调谐各参数让分子振动频率与高品质因数的八极子振荡频率相匹配,不仅有利于利用介电常数的变化检测周边环境的变化,还可以监控物质的太赫兹指纹谱。

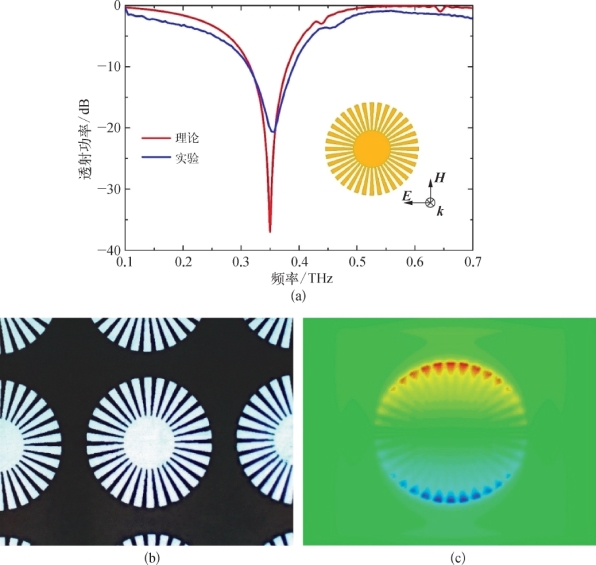
图5-5

(a)CMD的透射光谱在0.1～0.7 THz只有谐振;(b)SLSPs显微镜图像;(c)在0.35 THz处的电场分布

理论上SLSPs多极子的共振频率只要不超过相应的SSPPs的截止频率,相应的多极子共振都可以被激发。然而,CSR共振频率在激发多极子共振中起着重要作用。如果CSR共振频率远离结构的截止频率,高阶极子共振则很难被有效激发。而当CSR共振频率与结构截止频率重叠时,SLSPs模式与CSR模式(M)发生相互作用。根据图5-6,可知最高阶极子是十极。因为当SLSPs共振频率接近截止频率时,最高阶SLSPs的强度变弱,所以最高阶共振(C5)由于聚酰亚胺损耗和加工误差的附加损失几乎无法观察到。

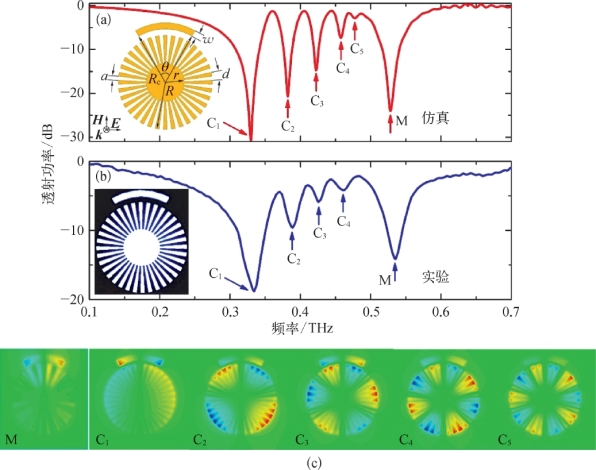
图5-6

CSR结合CMD的混合结构的理论(a)和实验(b)透射光谱,多极子共振电场分布图(c)显示为偶极子(C1)、四极子(C2)、六极子(C3)、八极子(C4)、十极子(C5)模式,共振(M)来自单一CSR结构支持的明态LSPs模式

(2)缺陷偶极子激发

带缺陷的人工原子SLSPs也能激发THz频段的多个Fano共振。当楔形切片以小角度切割时,可以产生多极Fano共振(四极到十极模式)。Fano共振是由楔形切片边缘支持的明态偶极子模式和暗态多极子模式的干涉造成的。与之前带CSR的混合结构相比,带缺陷的CMD具有新的有趣的光学性质,这是因为没有任何其他附加的明态偶极子(例如CSR)的共振频率可能与暗态多极子共振频率重叠,高阶Fano共振不会受到附加结构的共振频率的影响。另外,四极峰表现出高Q值特征,这种SLSPs结构可用于生物化学传感器。

图5-7给出了具有缺陷角度θ的人工粒子的几何形状,其外半径R为150μm,内半径r为60μm。内外半径间由36个周期金属槽组成(周期d=2πR/N)。a=0.4d代表单个周期结构中的沟槽宽度,金属膜(铝,σAl=3.56×107S·m-1)的厚度t=200 nm。衬底采用22μm厚的聚酯薄膜材料,该人工粒子阵列的周期是360μm。使用CST Microwave Studio进行数值模拟以获得对称(θ=0°)和有缺陷(θ=14°)的CMD结构的透射响应,其中E场极化垂直于有缺陷的楔形切片,如图5-8所示。在对称CMD中发现在0.369 THz处有明显的强偶极共振。然而,当电场垂直于缺陷时,通过自由空间THz波可以激发多个暗态多极子共振。多个Fano共振是由楔形缺陷边缘分布的明态偶极子模式与其余褶皱金属部分的暗态多极子模式之间的相互作用产生的。为了明确这种多个Fano共振的方向,图5-9显示了在谐振谷处的电场分布(线)和表面电流密度分布(1,0.36 THz;2,0.399 THz;3,0.444 THz;4,0.483 THz),四种谐振模式对应于偶极(1)、四极(2)、六极(3)和八极(4)共振模式。图5-9(下)表示在楔形缺陷边缘处的表面电流密度方向,表明对称性破坏(黑色虚线和箭头)时出现明态偶极子模式。如图5-9(a)所示,偶极子缺陷V形模式和偶极子SLSPs模式的电场线(箭头)从正电荷(红色)传播并到达负电荷(深蓝色)。因此,模式1(偶极模式)对应于混合的明态模式,其中偶极子缺陷V形模式和偶极子SLSPs模式同相振荡。模式2(四极模式)对应于偶极子缺陷V形模式和四极子SLSPs模式耦合产生的四极子Fano共振。需要说明的是,因为偶极子缺陷V形模式与四极子SLSPs模式的偶极子和四极子强烈的相互作用,所以透射谱中偶极子和四极子模式非常明显[图5-9(a)(b)]。模式3和模式4的共振说明尽管两个Fano共振是由明态偶极子模式和多极SLSPs模式(六极和八极模式)之间的相互作用引起的,但楔形缺陷在一定程度上影响和破坏了六极和八极模式的对称分布特性,与常规的六极和八极模式相比,其电场分布显示出轻微变形,如图5-9(c)(d)所示,由于单个缺陷结构的不对称性,激发的六极和八极模式较弱。

图5-7　平面缺陷CMD结构和显微镜图像:r=60μm,R=150μm,d=2πR/36,a=0.4d

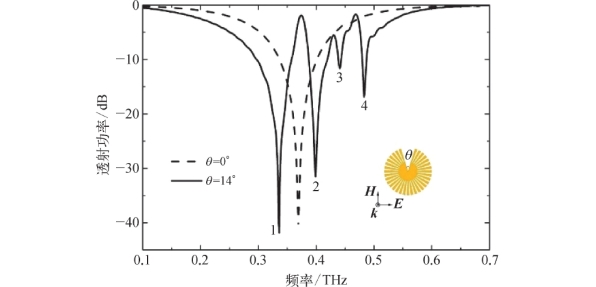
图5-8　在法向入射角下,对称(虚线)和缺陷角度为14°(实线)时CMD结构的模拟透射光谱。模式1、2、3和4分别对应偶极、四极、六极和八极模式(www.xing528.com)

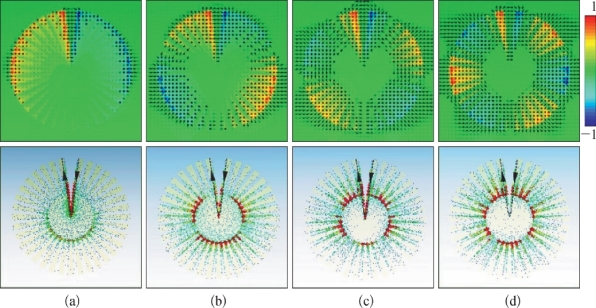
图5-9

偶极(a)、四极(b)、六极(c)、八极(d)模式的电场分布和表面电流密度分布的数值模拟结果。(上)偶极、四极、六极、八极模式的垂直电场分布,箭头表示电场线;(下)偶极、四极、六极、八极模式的表面电流密度分布,黑色虚线和箭头表示出现在楔形缺陷边缘的明态偶极子模式的方向

缺陷角度θ对暗态Fano共振具有重要影响。图5-10显示了x方向E场的具有不同缺陷角度的CMD的仿真透射图。从图中可以看到,缺陷切片边缘附近的共振模式3(4)较弱,这是由于六极(八极)Fano共振产生畸变。随着缺陷角的增加,共振模式3(4)变弱。相反地,混合偶极子模式和四极Fano共振变强。

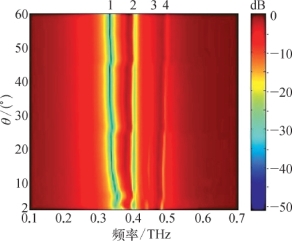
图5-10　x方向E场的具有不同缺陷角度的CMD的仿真透射图

这些多极子共振也可以通过实验观察到。我们使用常规光刻技术制造有缺陷的CMD(结构的显微镜图像如图5-7所示)。样品的尺寸为10 mm×10 mm。使用共聚焦8f太赫兹时域光谱系统测量样品的振幅透射光谱。图5-11(a)显示了通过空白聚酯薄膜衬底(参考样品)和带缺陷的CMD样品的透射太赫兹时域脉冲。图5-11(a)中的插图显示了从0 ps到20 ps的放大太赫兹时域脉冲,由于扫描时间为200 ps,光谱分辨率可以达到5 GHz。图5-11(b)显示了参考样品和带缺陷的CMD样品(θ=14°)的相应的傅里叶变换频域透射谱。归一化透射率如图5-11(c)所示,从图中可以清楚地观察到强偶极子模式、四极共振模式以及弱的六极和十极谐振模式。在模拟谱和实验谱中,六极和八极模式较弱,如图5-11(c)(d)所示,这与之前的理论分析一致。在图5-11(b)中,从0.325 THz到0.425 THz的四极子的峰值显示Q值高达30。这种高Q值性能具有超灵敏的共振传感,不仅可以探测附着在人工原子表面的薄膜(物质)的光学特性,还可以通过将原子的Fano共振频率设计在接近物质吸收峰的邻近位置来探测样品的性质以及监控分解物层的降解特性和固体(液体化合物)的动态化学反应过程。此外,通过结构化表面与特异性噬菌体结合,可以实现细菌的选择性检测(Fano共振位置的变化可能与细菌样品的浓度直接相关),从而实现细菌病原体的高效无标记检测。

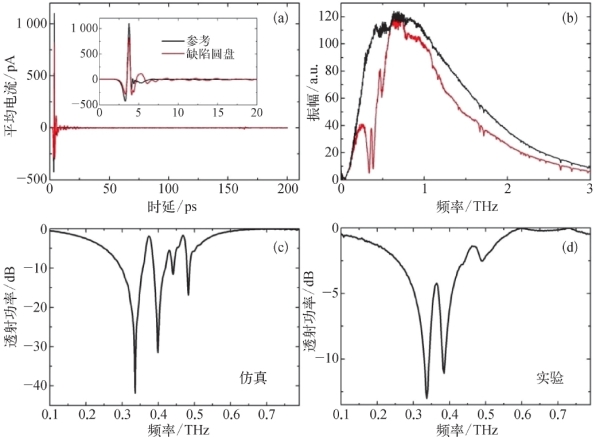
图5-11　实验测量的带缺陷的CMD样品的时域谱和频域谱

(a)参考样品和带缺陷的CMD样品的透射太赫兹时域脉冲;(b)频域透射谱;(c)理论值;(d)实验值

(3)波导结构激发

图5-12(a)是SSPPs波导激发SLSPs结构示意图。该结构包括三个部分:(1)能量转换部分[图5-12(b)];(2)模式转换和能量匹配部分[图5-12(c)];(3)SSPPs波导和谐振环[图5-12(d)]。端口1和端口2分别作为信号输入、输出端口。

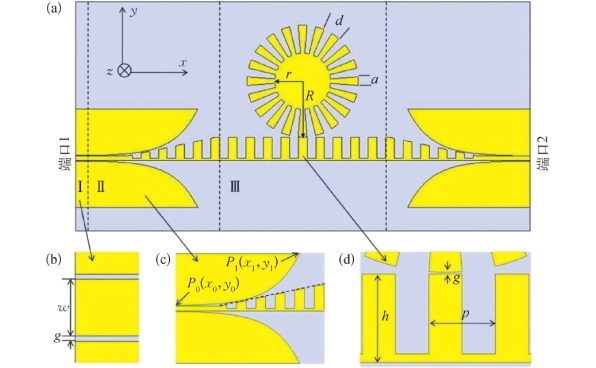
图5-12

(a)SSPPs波导激发SLSPs结构示意图;(b)能量转换部分;(c)模式转换和能量匹配部分;(d)SSPPs波导和谐振环

第(1)部分能量转换部分是共面波导(Coplanar Waveguide,CPW),能够传输QTEM模式的导波。共面波导的阻抗匹配由端口的参数决定,波导端口的宽度w为100μm,端口处的狭缝宽度g为9.4μm,石英衬底的介电常数ε为3.75。这样的参数设定满足端口50Ω的阻抗匹配。第(2)部分是模式转换和能量匹配部分,将QTEM模式的导波转换为SSPPs模式,参见第2章的共面波导激发SSPPs部分。第(3)部分是SSPPs波导和谐振环,这里波导作为一条传输线,支持SSPPs的传播。波导和谐振环之间的间隙为g。沟槽的宽度和周期分别表示为a=0.5d,p=2πR/N,其中N为谐振环沟槽的总数目(N=20)。谐振环和波导的沟槽d≪λ(λ为自由空间的波长)。波导的高度为h,谐振环的外径R=1 200μm,内径r=600μm,其他结构参数为h 1=500μm,h 2=450μm,p=380μm。利用CST微波工作室软件仿真,边界条件x、y、z设置为开放,模拟波在自由空间中传播。选择金作为表面层金属材料,是因为金的损耗小,而且在可见光范围内可看作完美电导体。选择石英作为基底材料,是因为石英的正切损耗很小,tanδ=0.000 4。金层的厚度为0.5μm,通过传统的光刻镀膜工艺附在石英表面。为了减少损耗,还可以用一些性能优良的低损介质,例如砷化镓和蓝宝石。本实验选用厚度为200μm的石英作为基底。仿真所得的传输系数(S 21参数)如图5-13(a)所示,红色曲线表示SSPPs波导和谐振环相互耦合作用所得的S 21参数,黑色曲线表示无谐振环时,仅SSPPs作为宽带传输的S 21参数。SSPPs波导和谐振环相互耦合产生6个明显的谐振谷。当谐振环越贴近SSPPs波导时,相互耦合作用产生的谐振谷越明显。此处谐振环与SSPPs波导的距离为9.4μm。不同的谷对应不同的模式,如图5-13(b)～(g)所示,电场平面扫描高度设置在距x-y平面上0.1 mm处。图5-13(a)中的谐振谷1～6对应图5-13(b)～(g)中的共振模式。图5-13(d)～(f)表明谐振谷3～5对应的谐振频率在波导端口2处无信号传输。谐振环附近的相位变化可以用以下公式计算:式中,n e为有效折射率,从SLSPs的色散曲线可以得出各模式的有效折射率n e;λ是自由空间的波长。当谐振环处于闭合状态时,输出端口无信号输出,此时Δφ=(2m+1)π,其中,m是模式数(m=0,1,2,3,…)。式(5-17)可写为2πRn e=(2m+1)λ/2,其中,n e=β/k,β是传播常数,k是波数。从而β=(2m+1)/2R,k=(2m+1)/2N。当谐振环处于闭合状态时,k和m之间的相对关系如表5-1所示。

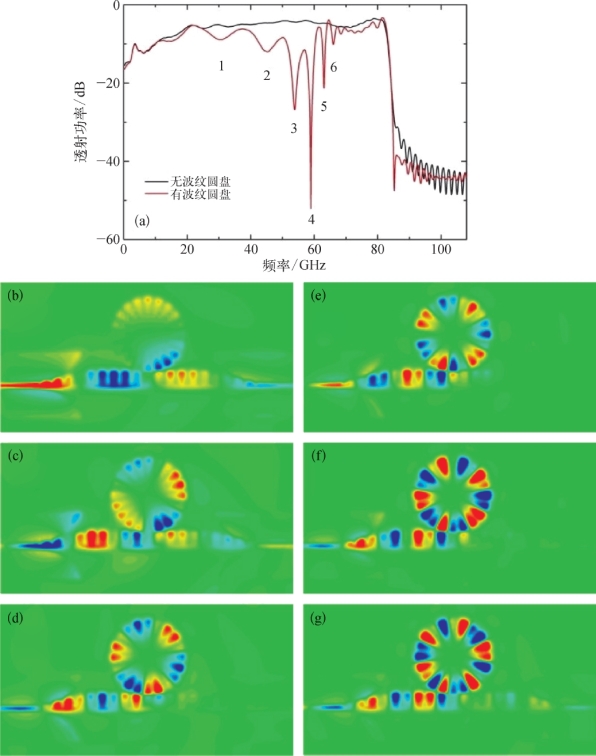
图5-13

(a)仿真所得的传输系数(S 21参数);(b)～(g)距x-y平面上0.1 mm处z方向的电场分布图

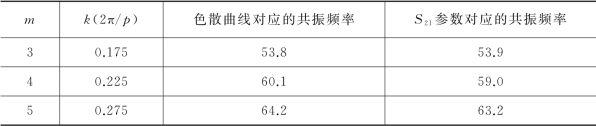
表5-1　k和m之间的相对关系

从表5-1可以推出,当谐振环处于闭合状态时,色散曲线和S 21参数对应的共振频率吻合,这证明理论结果和仿真结果基本一致。

实验中,采用15 mm×15 mm的石英作为基底。传感器芯片的成品图如图5-14(a)～(d)所示。S 21参数由频段50～75 GHz的安捷伦矢量网络分析仪(N5245A)测量。将探针的引脚分别置于端口1和端口2处,实验结果如图5-14(e)所示。谐振谷3～5出现在53.7 GHz、59.2 GHz、63.3 GHz,对应的S 21参数的值为-28.6 dB、-39.8 dB、-18.1 dB。

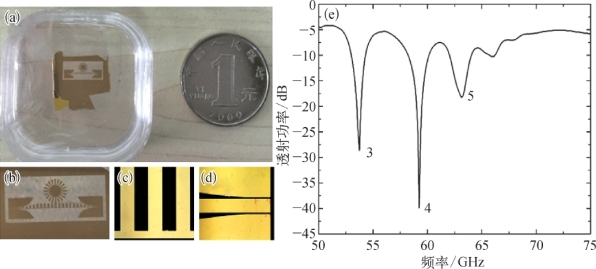
图5-14

(a)～(d)传感器芯片的成品图;(e)透射功率随频率变化的实验图

CMD对周围材料的变化敏感。如果改变CMD内的介电常数ε,那么共振频率将发生偏移。仿真结果表明六极子和八极子的共振频率偏移量为0.22 GHz(介电常数从ε=1.02变化到ε=1.1)。在图5-15中,当增加ε时,共振频率发生红移。

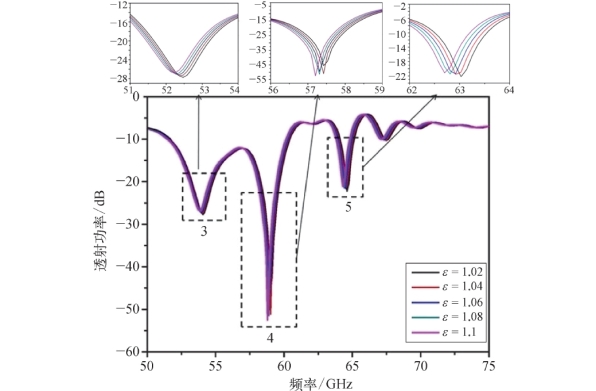
图5-15　共振频率随介电常数的变化

在实验中,我们用蘸有乙醇、去离子水和橄榄油等液体样品的棉签覆盖芯片中的CMD。当更换液体时,我们将传感器样品置于丙酮中,再置于去离子水中,最后用低功率超声波清洗机清洁样品。图5-16为实验结果,三种液体可以很明显地区分出来。在样品覆盖整个芯片区域和仅覆盖CMD的两种情况下,可以用Δf/(RIU/V)来估计Fano共振结构的灵敏度,其中V表示有效体积。当折射率为1.17(橄榄油)时,六极子谐振谷的偏移量在两种情况下分别为3.1 GHz和1.12 GHz。在第二种情况下,样品的体积要小得多。为消除体积的影响,我们计算了单位体积的灵敏度。如果样品厚度为5μm,则当整个芯片被橄榄油覆盖时产生的灵敏度为0.016 2(GHz/RIU)/(mm2×μm),而在只有CMD被橄榄油覆盖的情况下则为0.292(GHz/RIU)/(mm2×μm),灵敏度提高了17倍。

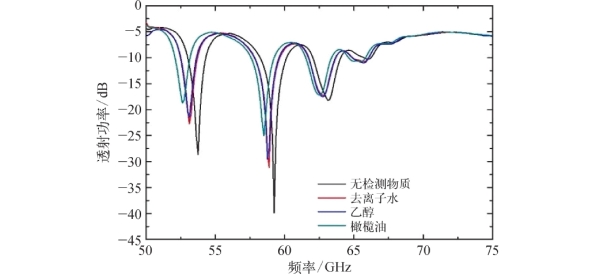
图5-16　对波纹圆盘中不同液体的探测