太赫兹表面等离激元在二维金属PCS传输中的特性

金属PCS由于其在滤波、极化、传感、成像等领域的广泛应用,已成为热门的研究领域。因此,如何设计和分析金属PCS中的光子能带结构和表面波特性显得十分重要。在本节中,我们重点介绍基于三角形晶格的金属PCS的超常透射、光子能带和表面波特性。首先,我们对金属PCS建模,解释超常透射机理;然后,我们推导和讨论光子能带沿着ΓM和ΓK晶格方向的能带图,分析不同的表面波特征;最后解释非对称入射下观察到的ΓM和ΓK晶格方向上的模式分裂效应。我们建立了描述这种模式分裂效应的精确的表面模式谐振频率公式,并对金属PCS的色散进行了定量分析。以上的研究结果推动了金属PCS的应用,并在THz功能器件领域有着广泛的应用。

金属PCS的周期性排布可以使用正方形或三角形网格。该结构能在THz波段形成带通传播通道。入射角度、通孔形状、几何尺寸、排列周期和孔内介质都会对其传输特性产生影响。如图4-5所示,本节研究采用圆孔、三角形网格,材质为纯铝,其表面镀铬防止氧化。

图4-5　金属圆孔阵列周期性排布示意图

金属PCS结构示意图如图4-6所示。图中给出的金属PCS由在铝(Al)板上的三角形孔阵列组成,尺寸为t=0.25 mm,d=0.7 mm,p=1.13 mm。THz波垂直入射到金属PCS上(蓝色入射波)。金属PCS几何尺寸为50 mm,保证周期数量。

图4-6　尺寸为t=0.25 mm、d=0.7 mm和p=1.13 mm的金属PCS结构的示意图,以及THz波沿着垂直方向(蓝色),与x轴呈θ角(ΓM)、与y轴呈θ角(ΓK)方向斜入射的示意图

ΓK和ΓM方向已在图4-6中标出。考虑到金属PCS中的波矢和入射波波矢之间的相互作用及匹配条件,入射THz波在金属PCS上与光栅常数p、入射角θ等参数密切相关,则金属PCS平面上的表面波矢量k sur可表示如下:

式中,m和n是整数;k x表示x方向传播的波矢分量,可以定义为

式中,k∥表示平行于金属PCS的表面波矢;G x和G y分别是六边形网格中沿x和y方向的倒格矢,可以表示为

则式(4-4)可以改写为

当电磁波从外部入射时,金属PCS可以支持表面波,这种表面波在金属和空气的界面处传播,并耦合到自由空间中。在孔的直径趋近于零时,表面波波矢可以表示为

式中,k sp为表面波共振矢量;f sp为表面波的谐振频率;c为真空中的光速;ε1为覆盖金属PCS的材料的介电常数;ε2=εr2+iεi2是金属介电常数(εr2和εi2分别是金属介电常数的实部和虚部)。Al的介电常数在1 THz波段为-44 900+i511 000,这比在可见光范围内的数值大得多,所以式(4-9)右边根号内的项可近似为1。

根据式(4-8)和式(4-9),我们画出了金属PCS在ΓM和ΓK方向的完整的光子能带图,如图4-7所示。为了方便起见,将图4-7中的色散图折叠到第一布里渊区里。在ΓM方向,有一个强的谐振峰色散线(红线)和三个弱的谐振峰色散线。红线对应的是表面波模式(-1,0),我们发现模式(-1,0)有陡峭的负斜率,与真空中的光色散线几乎相同。然而,在ΓK方向,有一个强的谐振峰色散线(蓝线)和两个弱的谐振峰色散线。蓝线对应于表面波模式(0,-1)。

图4-7　金属PCS在ΓM和ΓK方向的完整的光子能带图

接着,我们展示了表面波的共振峰随入射角的变化。THz波在ΓM和ΓK两个方向上以一定的入射角入射,如图4-6所示。表面波的谐振频率f sp不仅受孔阵的几何构造影响,还受入射角θ的影响。显而易见,k∥可以表示为(www.xing528.com)

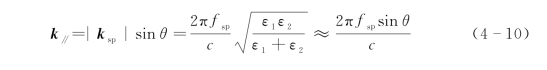
将式(4-9)和式(4-10)代入式(4-8)可得

于是式(4-11)和式(4-12)可以写成如下形式:

整理后可得

此一元二次方程的解为

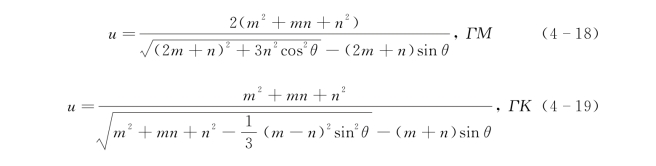
利用式(4-13)、式(4-18)和式(4-19),我们可以得到表面波的谐振频率为

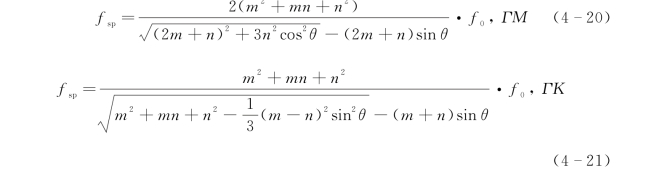
为了验证仿真结果,我们在实验中将金属PCS沿x轴(ΓM方向)和y轴(ΓK方向)旋转,以代替不同的THz波入射角。从图4-8中我们可以看到,当入射波不是垂直入射时,透射峰会分裂成两个峰,而峰值共振频率会发生红移。由式(4-20)和式(4-21)得到的金属PCS在表面波模式下的色散特性以及不同入射角产生的模式分裂效应如图4-9所示。当入射波垂直照射在表面时,THz波的能量与金属PCS的本征模耦合。随着入射角的改变,本征模会分为若干个模式,每个模式都有自身的色散曲线(图4-9)。本征模的分裂与布里渊区有关,这是由金属PCS的几何结构决定的。从图4-8和图4-9可以看出,当入射角改变时,金属PCS表面波模式的色散和与共振频率对应的真空中的光色散线之间的相互作用点发生了移动[图4-9(a)中的点A、B、C、D和图4-9(b)中的点E、F、G、H]和分离[图4-9(a)中的点A和I]。从图4-10可以看到,实验结果(以ΓM方向为例)与理论计算得到的结果相吻合。

图4-8

(a)沿x轴方向旋转时,THz波在金属PCS上透射的特性;(b)沿y轴方向旋转时,THz波在_金属PCS上透射的特性

图4-9　金属PCS表面波模式的色散(灰色线)

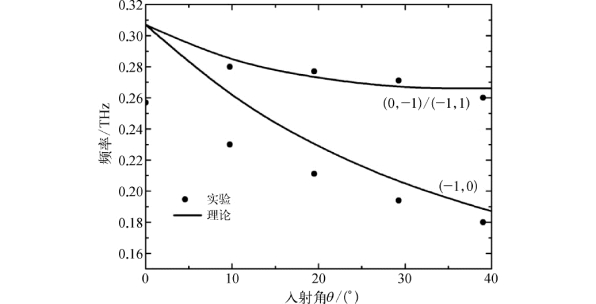
图4-10　当入射角θ从0°增加到40°时(ΓM方向),模式为(-1,0)和(0,-1)/(-1,1)的共振频率的变化:实线为理论计算得到的结果,点为实验结果